Výpočet Velikonoční neděle v gregoriánském kalendáři
Velikonoční neděle v juliánském kalendáři!
Popis výpočtu kalendářního data Velikonoční neděle v gregoriánském kalendáři pro daný rok je v principu stejný jako v juliánském kalendáři. Pomocí epakty nalezneme první jarní cyklický úplněk a následující nejbližší neděle je pak hledaná Velikonoční neděle. Při následujících výpočtech se vždy počítá pouze s celými čísly, znak '%' značí operátor zbytek po dělení. Zde je popsán původní výpočet gregoriánské epakty, tak jak je zapsán v díle od Christopha Claviuse (viz komise pro reformu kalendáře) ROMANI CALENDARII A GREGORIO XIII. P.M. RESTITUTI Explicatio. V této knize se však místo vzorců používají tabulky, kde naleznete potřebné hodnoty. Nejdříve nalezneme Zlaté číslo daného roku.
Nyní vypočteme takzvanou juliánskou epaktu. Konstanta 11, která se přičítá, byla zjištěna pozorováním skutečných novoluní v době gregoriánské reformy. Je to posun jen o tři dny oproti výpočtům ve starém juliánském kalendáři, ve skutečnosti se staré výpočty od astronomická skutečnosti v té době lišily až o čtyři dny. Podle starých tabulek připadalo první novoluní v roce pro Zlaté číslo 1 na den 23. ledna, viz chronologická tabulka. Po vypuštění deseti dnů při reformě by se posunulo na 2. února, takže by mu předcházelo ještě jedno novoluní, které by bylo 3. ledna. Lilius pak cyklické novoluní pro gregoriánskou epaktu 1 posunul o tři dny nazpět (0. leden≡31. prosinec), více na stránce Porovnání juliánských a gregoriánských cyklických výpočtů. Samotná juliánská epakta ukazuje na o tři dny opravená novoluní v juliánském kalendáři.
což lze zjednodušit na juliánská_epakta = 11 × zlaté_číslo % 30
nebo jinak: juliánská_epakta = (11 × (rok % 19) + 11) % 30
Pak lehce vypočteme následující tabulku, kde ke každému zlatému číslu je jednoznačně přiřazena juliánská epakta.:
| Zlaté číslo | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| juliánská epakta | 11 | 22 | 3 | 14 | 25 | 6 | 17 | 28 | 9 | 20 | 1 | 12 | 23 | 4 | 15 | 26 | 7 | 18 | 29 |
| Zlaté číslo | juliánská epakta |
| 1 | 11 |
| 2 | 22 |
| 3 | 3 |
| 4 | 14 |
| 5 | 25 |
| 6 | 6 |
| 7 | 17 |
| 8 | 28 |
| 9 | 9 |
| 10 | 20 |
| 11 | 1 |
| 12 | 12 |
| 13 | 23 |
| 14 | 4 |
| 15 | 15 |
| 16 | 26 |
| 17 | 7 |
| 18 | 18 |
| 19 | 29 |
Doposud byl postup podobný jako u juliánského kalendáře, nyní je zapotřebí provést opravu (vyrovnání) juliánské epakty, abychom dostali výslednou gregoriánskou epaktu. Nejdříve vypočteme století ve kterém je daný rok. V tomto výpočtu století začíná takzvaným centenárním rokem (centenární rok končí dvěma nulami, například 1900, 2000, 2100). A století končí 99, což je oproti běžnému pojmu století posun o jeden rok. Například 21. století jsou správně roky mezi 2001 a 2100 včetně. Ale pro následující výpočty bereme 21. století jako roky 2000 až 2099 včetně.
Protože v gregoriánském kalendáři jsou centenární roky přestupné pouze pokud jsou dělitelné 400, v cyklu 400 let vypadnou tři přestupné dny oproti juliánskému kalendáři. O tyto dny je zapotřebí epaktu zmenšit, jde o takzvanou sluneční opravu (vyrovnání) (aequatio solaris). Oprava se provádí v centenárních nepřestupných letech, tedy 1700, 1800, 1900, 2100, 2200 atd.:
Pro nejbližší století pak dostáváme hodnoty uvedené v tabulce, protože se tato oprava odečítá, jsou uvedeny jako záporné Hodnota postupně roste jak se vynechávají přestupné dny v centenárních letech. A protože rok při přechodu z 20. na 21. století (rok 2000) byl v gregoriánském kalendáři přestupný (stejně jako v juliánském), hodnota se nezměnila.
| století roky od do | 16. 1583-99 | 17. 1600-99 | 18. 1700-99 | 19. 1800-99 | 20. 1900-99 | 21. 2000-99 | 22. 2100-99 | 23. 2200-99 | 24. 2300-99 | 25. 2400-99 |
| sluneční oprava | 0 | 0 | -1 | -2 | -3 | -3 | -4 | -5 | -6 | -6 |
| století roky od do | sluneční oprava |
| 16. 1583-99 | 0 |
| 17. 1600-99 | 0 |
| 18. 1700-99 | -1 |
| 19. 1800-99 | -2 |
| 20. 1900-99 | -3 |
| 21. 2000-99 | -3 |
| 22. 2100-99 | -4 |
| 23. 2200-99 | -5 |
| 24. 2300-99 | -6 |
| 25. 2400-99 | -6 |
Protože ani 19-letý měsíční cyklus fází není přesný, po 19 letech přicházejí měsíční fáze o 1.5 hodiny dříve, chyba jednoho dne tak nastane po více jak 300 letech. Kalendářní komise nakonec rozhodla, že v cyklu 2500 letech se provede takzvaná měsíční oprava (vyrovnání) (aequatio lunaris) osmkrát, tedy v průměru jednou za 312.5 let. Oprava se provádí opět pouze v centenárních letech. Proto se oprava provedla či provede v letech 1800, 2100, 2400, 2700, 3000, 3300, 3600, 3900 (tedy po 300 letech), ale pak až roku 4300 (tedy po 400 letech). Po té se 2500-letý cyklus znovu opakuje.
Pro nejbližší století pak dostáváme hodnoty uvedené v tabulce:
| století roky od do | 16. 1583-99 | 17. 1600-99 | 18. 1700-99 | 19. 1800-99 | 20. 1900-99 | 21. 2000-99 | 22. 2100-99 | 23. 2200-99 | 24. 2300-99 | 25. 2400-99 |
| měsíční oprava | 0 | 0 | 0 | 1 | 1 | 1 | 2 | 2 | 2 | 3 |
| století roky od do | měsíční oprava |
| 16. 1583-99 | 0 |
| 17. 1600-99 | 0 |
| 18. 1700-99 | 0 |
| 19. 1800-99 | 1 |
| 20. 1900-99 | 1 |
| 21. 2000-99 | 1 |
| 22. 2100-99 | 2 |
| 23. 2200-99 | 2 |
| 24. 2300-99 | 2 |
| 25. 2400-99 | 3 |
Přehledně lze obě opravy prováděné v jednotlivých centenárních letech zobrazit v tabulce (s.o.:sluneční oprava, m.o.:měsíční oprava). Nezapomeňte na 'nepravidelnost' měsíční opravy, po roce 3900 nastane oprava až po 400 letech a ne jako většinou po 300 letech. Toto se opakuje každých 2500 let, tedy znovu v roce 6400.
| rok | s.o. | m.o. |
|---|---|---|
| 1600 | ||
| 1700 | -1 | |
| 1800 | -1 | +1 |
| 1900 | -1 | |
| 2000 | ||
| 2100 | -1 | +1 |
| 2200 | -1 | |
| 2300 | -1 | |
| 2400 | +1 | |
| 2500 | -1 | |
| 2600 | -1 | |
| 2700 | -1 | +1 |
| 2800 | ||
| 2900 | -1 | |
| 3000 | -1 | +1 |
| 3100 | -1 |
| rok | s.o. | m.o. |
|---|---|---|
| 3200 | ||
| 3300 | -1 | +1 |
| 3400 | -1 | |
| 3500 | -1 | |
| 3600 | +1 | |
| 3700 | -1 | |
| 3800 | -1 | |
| 3900 | -1 | +1 |
| 4000 | ||
| 4100 | -1 | |
| 4200 | -1 | |
| 4300 | -1 | +1 |
| 4400 | ||
| 4500 | -1 | |
| 4600 | -1 | +1 |
| 4700 | -1 |
| rok | s.o. | m.o. |
|---|---|---|
| 4800 | ||
| 4900 | -1 | +1 |
| 5000 | -1 | |
| 5100 | -1 | |
| 5200 | +1 | |
| 5300 | -1 | |
| 5400 | -1 | |
| 5500 | -1 | +1 |
| 5600 | ||
| 5700 | -1 | |
| 5800 | -1 | +1 |
| 5900 | -1 | |
| 6000 | ||
| 6100 | -1 | +1 |
| 6200 | -1 | |
| 6300 | -1 |
| rok | s.o. | m.o. |
|---|---|---|
| 6400 | +1 | |
| 6500 | -1 | |
| 6600 | -1 | |
| 6700 | -1 | |
| 6800 | +1 | |
| 6900 | -1 | |
| 7000 | -1 | |
| 7100 | -1 | +1 |
| 7200 | ||
| 7300 | -1 | |
| 7400 | -1 | +1 |
| 7500 | -1 | |
| 7600 | ||
| 7700 | -1 | +1 |
| 7800 | -1 | |
| 7900 | -1 |
| rok | s.o. | m.o. |
|---|---|---|
| 8000 | +1 | |
| 8100 | -1 | |
| 8200 | -1 | |
| 8300 | -1 | +1 |
| 8400 | ||
| 8500 | -1 | |
| 8600 | -1 | +1 |
| 8700 | -1 | |
| 8800 | ||
| 8900 | -1 | +1 |
| 9000 | -1 | |
| 9100 | -1 | |
| 9200 | ||
| 9300 | -1 | +1 |
| 9400 | -1 | |
| 9500 | -1 |
Poslední oprava je odečtení deseti dnů vypuštěných při gregoriánské reformě kalendáře. Tak získáme výslednou gregoriánskou epaktu.
je-li výsledek řádek menší jak 0, přičtěte 30 nebo je-li výsledek větší jak 29, odečtěte 30.
Níže je přehledná tabulka výsledku všech korekcí juliánské epakty pro gregoriánský kalendář pro nejbližší staletí. Někdy se opravy navzájem vyruší a výsledná korekce pak zůstane stejná, například při přechodu z 21. na 22. století se změní jak sluneční tak měsíční oprava. Ve výsledku se však vzájemně vyruší a korekce zůstává stejná.
| století roky od do | 16. 1583-99 | 17. 1600-99 | 18. 1700-99 | 19. 1800-99 | 20. 1900-99 | 21. 2000-99 | 22. 2100-99 | 23. 2200-99 | 24. 2300-99 | 25. 2400-99 |
| celková oprava | -10 | -10 | -11 | -11 | -12 | -12 | -12 | -13 | -14 | -13 |
| století roky od do | celková oprava |
| 16. 1583-99 | -10 |
| 17. 1600-99 | -10 |
| 18. 1700-99 | -11 |
| 19. 1800-99 | -11 |
| 20. 1900-99 | -12 |
| 21. 2000-99 | -12 |
| 22. 2100-99 | -12 |
| 23. 2200-99 | -13 |
| 24. 2300-99 | -14 |
| 25. 2400-99 | -13 |
Různá století tak mají své 19-leté řady epakt. Podstata však zůstává stejná jako u alexandrijských epakt. Hodnota roste po jednotlivých rocích devatenáctiletého kruhu Zlatého čísla po 11, jen na konci kruhu se zvětší o 12. Tento cyklus je přerušen při přechodu na jiné století, které má jinou opravu. Například rok 1862 má Zlaté číslo 1 a patří do 19. století. Gregoriánská epakta roku 1862 je 0. Následující rok se Zlatým číslem 1 je rok 1881 a protože patří též do 19. století má tutéž epaktu 0. Ale rok 1900, také se Zlatým číslem 1, patří již do 20. století (připomínám zvláštní definici století výše), kde je jiná oprava juliánské epakty a proto je výsledná gregoriánská epakta rovna 29. Výpis všech možných řad epakt naleznete na stránce Všechny možné řady gregoriánských epakt, níže je tabulka řad epakt jen pro nejbližší století. V 20., 21. a 22. století se řady epakt nemění, dá se říci, že z hlediska řad gregoriánských epakt žijeme v klidné době.
| Zlaté číslo | jul. epakta | 16. 1583-99 | 17. 1600-99 | 18. 1700-99 | 19. 1800-99 | 20. 1900-99 | 21. 2000-99 | 22. 2100-99 | 23. 2200-99 | 24. 2300-99 | 25. 2400-99 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 11 | 1 | 1 | 0 | 0 | 29 | 29 | 29 | 28 | 27 | 28 |
| 2 | 22 | 12 | 12 | 11 | 11 | 10 | 10 | 10 | 9 | 8 | 9 |
| 3 | 3 | 23 | 23 | 22 | 22 | 21 | 21 | 21 | 20 | 19 | 20 |
| 4 | 14 | 4 | 4 | 3 | 3 | 2 | 2 | 2 | 1 | 0 | 1 |
| 5 | 25 | 15 | 15 | 14 | 14 | 13 | 13 | 13 | 12 | 11 | 12 |
| 6 | 6 | 26 | 26 | 25 | 25 | 24 | 24 | 24 | 23 | 22 | 23 |
| 7 | 17 | 7 | 7 | 6 | 6 | 5 | 5 | 5 | 4 | 3 | 4 |
| 8 | 28 | 18 | 18 | 17 | 17 | 16 | 16 | 16 | 15 | 14 | 15 |
| 9 | 9 | 29 | 29 | 28 | 28 | 27 | 27 | 27 | 26 | 25 | 26 |
| 10 | 20 | 10 | 10 | 9 | 9 | 8 | 8 | 8 | 7 | 6 | 7 |
| 11 | 1 | 21 | 21 | 20 | 20 | 19 | 19 | 19 | 18 | 17 | 18 |
| 12 | 12 | 2 | 2 | 1 | 1 | 0 | 0 | 0 | 29 | 28 | 29 |
| 13 | 23 | 13 | 13 | 12 | 12 | 11 | 11 | 11 | 10 | 9 | 10 |
| 14 | 4 | 24 | 24 | 23 | 23 | 22 | 22 | 22 | 21 | 20 | 21 |
| 15 | 15 | 5 | 5 | 4 | 4 | 3 | 3 | 3 | 2 | 1 | 2 |
| 16 | 26 | 16 | 16 | 15 | 15 | 14 | 14 | 14 | 13 | 12 | 13 |
| 17 | 7 | 27 | 27 | 26 | 26 | 25 | 25 | 25 | 24 | 23 | 24 |
| 18 | 18 | 8 | 8 | 7 | 7 | 6 | 6 | 6 | 5 | 4 | 5 |
| 19 | 29 | 19 | 19 | 18 | 18 | 17 | 17 | 17 | 16 | 15 | 16 |
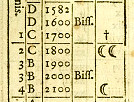
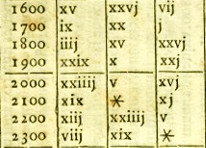
Gregoriánská epakta může nabývat hodnot 0 až 29, stejně jako alexandrijská z výpočtu Velikonoční neděle v juliánském kalendáři. V některých pramenech se místo 0 používá 30, ale původně se používala hvězdička a ostatní čísla epakt byla zapsána římskými číslicemi. V daném století se však používá jen 19 různých hodnot. Ale s celkem 30 hodnotami gregoriánské epakty nastává potíž, ze starého juliánského výpočtu totiž víme, že cyklický úplněk může nastat mezi 21. březnem a 18. dubnem, to je celkem 29 dnů. Zatímco ve výpočtu pro juliánský kalendář bylo 19 možných alexandrijských epakt bez problému rozděleno mezi oněch 29 dnů, u 30 gregoriánských epakt to již tak jednoduché pochopitelně není. Tento rozsah 29 dnů musel být dle přání církve zachován i v novém gregoriánském kalendáři. Dřívější termín nepřipadal v úvahu, neboť by byl před církevním začátkem jara. A pokud by byl nejpozdější termín prodloužen na 19. duben, mohl by nastat případ, kdy by byla Velikonoční neděle až 26. dubna. Jestliže totiž cyklický úplněk nastane v neděli, je Velikonoční neděle až o týden později. Z obavy, že by z tohoto důvodu mnozí lidé nový kalendář nepřijali, byla i tato možnost zavržena. Navíc církev vyžadovala, aby se v jednom devatenáctiletém kruhu Zlatého čísla nevyskytoval nejpozdější termín Velikonoční neděle dvakrát.
Proto byla nakonec vybrána epakta 25, které jsou přiřazena dvě možná kalendářní data cyklického úplňku, 17. nebo 18. duben. Pomocí následujícího pravidla určíme jaké datum použít: pokud je Zlaté číslo větší nebo rovno 12, vybere se datum 17. duben, jinak se vybere 18. duben. Tímto se zamezí opakovaní nejpozdějšího termínu Velikonoční neděle v devatenáctiletém cyklu. Více o tomto problému na stránce Epakta 25. Pokud je to nutné, je na tomto webu epakta s dřívějším datem cyklického úplňku (tedy Zlaté číslo větší jak 11) psána tučným písmem - 25.
Každé hodnotě epakty můžeme jednoznačně přiřadit datum cyklického úplňku, s výjimkou epakty 25, které lze přiřadit dvě kalendářní data.
| epakta | 23 | 22 | ... | 2 | 1 | 0 | 29 | 28 | 27 | 26 | 25/25 | 24 |
| datum úplňku | 21.3. | 22.3. | ... | 11.4. | 12.4. | 13.4. | 14.4. | 15.4. | 16.4. | 17.4. | 17./18.4. | 18.4. |
| epakta | datum úplňku |
| 23 | 21.3. |
| 22 | 22.3. |
| ... | ... |
| 2 | 11.4. |
| 1 | 12.4. |
| 0 | 13.4. |
| 29 | 14.4. |
| 28 | 15.4. |
| 27 | 16.4. |
| 26 | 17.4. |
| 25/25 | 17./18.4. |
| 24 | 18.4. |
Vidíme například, že nejdřívější cyklický úplněk, potažmo Velikonoční neděle, může nastat jen při epaktě 23. V tabulce gregoriánských řad epakt se tato epakta vyskytuje například v 19. století a pak až ve 23. století. To vysvětluje velkou mezeru mezi nejdřívější možnou Velikonoční nedělí (22. března), která byla naposledy v roce 1818 a bude zase až v roce 2285. Protože se ve 20. až 22. století epakta 23 nevyskytuje, nemůže ani nastat nejdřívější datum Velikonoční neděle, máme smůlu.
Datum úplňku lze pak určit dle tabulky na stránce Online výpočet Velikonoční neděle dole, nebo výpočtem:
pro epaktu 24: den_úplňku = 49
pro epaktu 25 a Zlaté číslo < 12: den_úplňku = 49
pro epaktu 25 a Zlaté číslo >= 12: den_úplňku = 48
pro epaktu 26 - 29: den_úplňku = 74 - epakta
Je-li výsledkem číslo větší jak 31, cyklický úplněk začíná až v dubnu, dubnové datum pak dostaneme po odečtení 31 od výsledku. Zbývá už jen určit kolikátým dnem týdne je den úplňku, abychom určili následující neděli. V gregoriánském kalendáři lze použít vzorec z juliánského kalendáře, kde navíc odečteme rozdíl ve dnech mezi oběma kalendáři (takzvaná gregoriánská oprava).
den_týdne = (rok + rok / 4 - gregoriánská_oprava + den_úplňku) % 7
Číslo 0 je neděle, 1 pondělí a tak dál až do 6, což je sobota.
Kalendářní datum Velikonoční neděle v gregoriánském kalendáři pak dostaneme snadno:
dostaneme-li číslo větší jak 31, jde o dubnové datum - nutno pak odečíst 31,
jinak jde o březnové datum
Poznámka:
Na internetu lze najít podobný výpočet gregoriánské epakty, který se liší jen konstantami, výsledek je pochopitelně stejný. Používá se alexandrijská epakta a k ní se přičítají opravy s jinými hodnotami, výsledek je zase gregoriánská epakta.
sluneční_oprava2 = 3 × století / 4
měsíční_oprava2 = (8 × století + 5) / 25
gregoriánská epakta = alexandrijská_epakta - sluneční_oprava2 + měsíční_oprava2 + 8
Důrazně upozorňuji na jiné hodnoty jednotlivých oprav, oproti hodnotám uvedených v knize Explicatio. Konstanta 8 je rozdíl mezi alexandrijskou a gregoriánskou epaktou pro 1. leden v chronologické tabulce. Ten den má gregoriánská epakta hodnotu 0, Zlaté číslo juliánského kalendáře pro tento den je 3. Zlatému číslu 3 lze přiřadit alexandrijskou epaktu 22, výpočet viz stránka Výpočet Velikonoční neděle v juliánském kalendáři. Musíme tedy přičíst 8, abychom dostali hodnotu gregoriánské epakty v témže dni (30≡0).
Protože dostanete jinou hodnotu sluneční opravy, vypočtěte gregoriánskou opravu (nutnou pro zjištění dne v týdnu, kdy nastane cyklický úplněk) podle upraveného vzorce. Výsledek je stejný, tedy rozdíl ve dnech mezi juliánským a gregoriánským kalendářem pro dané století.
Zbývající vzorce jsou již stejné.
Další informace:
- Velikonoce
- Online výpočet Velikonoční neděle
- Rozložení Velikonočních nedělí v závislosti na epaktě graficky
- Velikonoční neděle gregoriánského kalendáře
- Ostatní algoritmy výpočtu Velikonoční neděle
- Všechny možné řady gregoriánských epakt
- Epakta 25
- Kalendářní data Velikonoční neděle
- Tabulka epakt a cyklických úplňků
- Velká tabulka kalendářních dat
- Výskyty Velikonoční neděle pro jednotlivé dny v letech 1801 až 2300
- Základy roku
- Zlaté číslo
- Chronologická tabulka
- Tabulka cyklických novoluní
- Gregoriánská reforma kalendáře
- Komise pro reformu kalendáře
- Porovnání juliánských a gregoriánských cyklických výpočtů
- Inter gravissimas
- Výpočet Velikonoční neděle v juliánském kalendáři
- Převod mezi kalendáři
- Kalendářní data katolických a pravoslavných Velikonoc
- Přesnost kalendářů