Rozložení Velikonočních nedělí v závislosti na epaktě graficky

Velikonoční neděle je následující neděle po první jarním cyklickém úplňku. Každé epaktě je přiřazeno datum cyklického úplňku, který musí nastat někdy mezi 21. březnem a 18. dubnem včetně. Cyklický úplněk může nastat v libovolném dnu týdne. Pokud nastane v neděli, tak až ta následující neděle se stává Velikonoční nedělí. Proto se datum Velikonoční neděle vyskytuje mezi 22. březnem a 25. dubnem. Z toho plyne, že datum Velikonoční neděle závisí na epaktě a dnu týdne, kdy nastal cyklický úplněk - potažmo tedy na nedělním písmenu. V případě přestupného roku na tom druhém písmenu, neboť Velikonoční neděle je vždy po přestupném dni. Nalezení kalendářního data Velikonoční neděle podle těchto dvou údajů si můžete vyzkoušet třeba v historické tabulce Tabula Paschalis Nova Reformata.

Můžeme si zhotovit graf, kde každému kalendářnímu datu Velikonoční neděle jsou přiřazeny gregoriánské epakty, pro které může nastat právě toto datum. V prvním sloupci jsou všechna možná kalendářní data Velikonoční neděle, v druhém nedělní písmena. V barevných obdélnících je pak číslo gregoriánské epakty. Šířka obdélníku (a pro zvýraznění též jeho barva) zobrazuje kolikrát se tato epakta vyskytne pro dané datum v celém cyklu Velikonoc, jenž je dlouhý 5 700 000 let.

Například Velikonoční neděle dne 23. března může nastat pouze při epaktě 23 nebo 22, v celém cyklu Velikonoc nastane tato možnost 54150× (27075+27075). Naposledy se tak stalo v roce 2008, tento rok měl gregoriánskou epaktu 22 a nedělní písmeno FE.

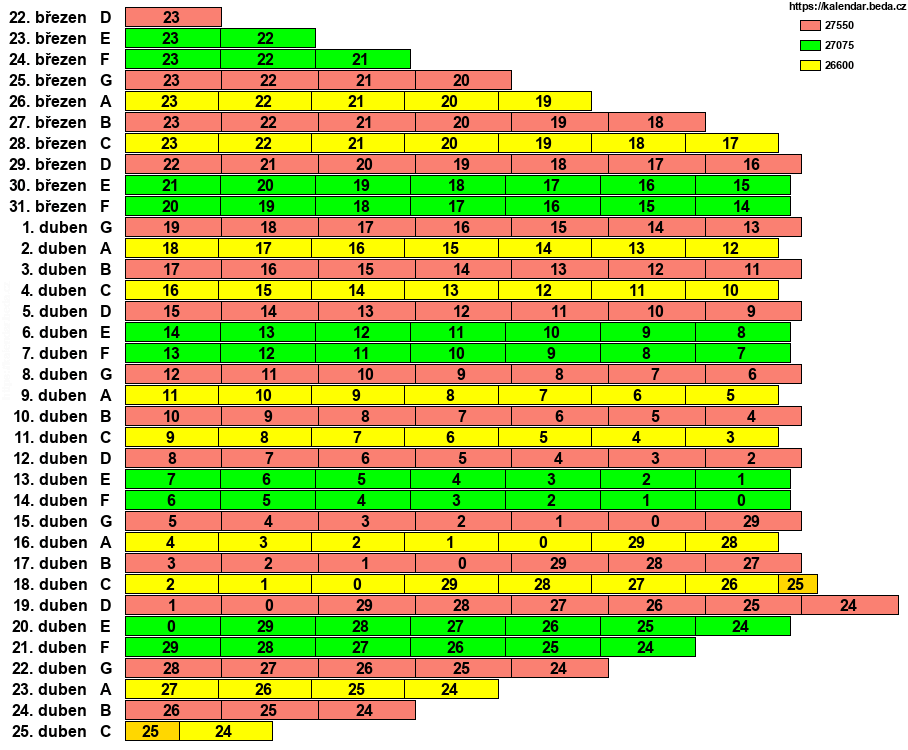
Rozložení Velikonočních nedělí v gregoriánském kalendáři v závislosti na epaktě graficky

Doposud to bylo docela jednoduché, existují však dvě výjimky, které to trochu komplikují. Jak už víme, cyklický úplněk může nastat mezi 21. březnem a 18. dubnem, to je celkem 29 dnů. Ale epakt je 30. Nejjednodušším řešením by bylo dovolit cyklický úplněk pro poslední epaktu 24 dne 19. dubna, ale to by pak Velikonoční neděle mohla nastat i 26. dubna a to bylo nepřijatelné. Proto se v případě epakty 24 cyklický úplněk posouvá o jeden den zpět. Většinou to nevadí, například kdyby měl nastat cyklický úplněk epakty 24 v pátek, tak se posunutím o jeden den zpět na čtvrtek, datum Velikonoční neděle nezmění. Ale pokud by měl nastat cyklický úplněk epakty 24 v neděli (Velikonoční neděle je pak až příští neděli), tak posunutím o jeden den zpět (na sobotu) poskočí datum Velikonoční neděle o celý týden zpět. A proto je u 19. dubna epakta 24 navíc a díky tomu je také tento termín Velikonoční neděle nejčastější možný v celém cyklu Velikonoc. Naposledy se tak stalo v roce 1981 a příště se tak zase stane v roce 2076.

Díky tomuto řešení pak poslední termín Velikonoční neděle (25. duben) mohl nastat při epaktě 25 a 24. Což byla zase potíž, protože v jednom cyklu Zlatého čísla mohl nastat tento nejzazší termín dvakrát a to církev odmítala. Ze stránky Epakta 25 víme, že tyto dvě epakty se sejdou v jednou cyklu Zlatého čísla pouze pokud je Zlaté číslo pro daný rok větší nebo rovno 12. A proto se právě v tomto případě opět posune datum cyklického úplňku o den zpět. Což je ve výjimečném případě (stejný důvod jako u epakty 24, viz výše) příčinou změny termínu Velikonoční neděle o jeden týden zpět na 18. duben. Naposledy se tak stalo v roce 1954 a příště se tak zase stane v roce 2049.

Srovnejte tento graf s jednodušším grafem na stránce Výskyty Velikonoční neděle pro jednotlivé dny v celém cyklu Velikonoc gregoriánského kalendáře. Přesná čísla jednotlivých výskytů najdete zase v tabulce na stránce Rozložení Velikonočních nedělí v závislosti na epaktě. Metodu jak tyto výskyty vypočítat naleznete na stránce Výpočet frekvence rozložení Velikonočních nedělí gregoriánského kalendáře.

Jen pro zajímavost si můžeme ukázat jak by výše zobrazený graf vypadal bez těchto dvou výjimek, tedy i s možností Velikonoční neděle dne 26. dubna. Jde však jen o hypotetický kalendář, nic takového neplatí. Ale graf je o něco jednodušší.

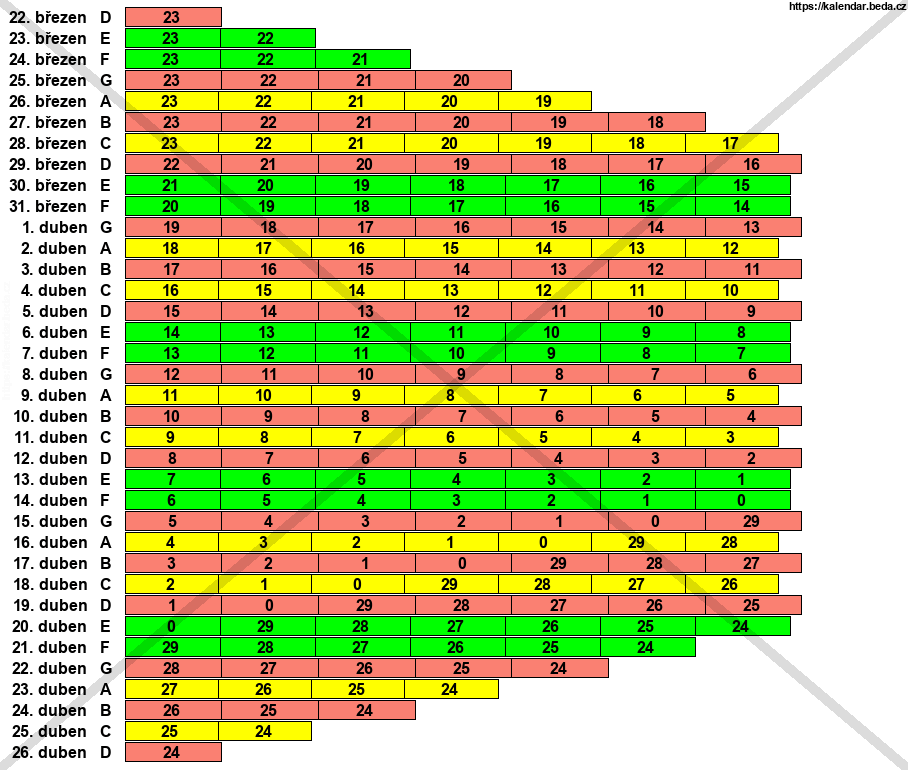
Rozložení Velikonočních nedělí v hypotetickém kalendáři v závislosti na epaktě graficky

Rozložení Velikonočních nedělí v hypotetickém kalendáři (kde může být Velikonoční neděle i 26. dubna) v závislosti na epaktě graficky

Rozložení Velikonočních nedělí v závislosti na epaktě graficky

Další informace: