Židovský kalendář
Obsah
- Historie
- Židovské svátky
- Pravidla pro výpočty v židovském kalendáři
- Určení prvního dne roku
- Keviah: typ roku
- Čtyři brány židovského kalendáře
- Tekufy: roční doby
- Cykly židovského kalendáře
Historie
Židovský kalendář je babylónského původu a je především kalendářem náboženským. Jde o lunisolární kalendář, délka kalendářních měsíců odpovídá délce lunace a průměrná délka roku je podobná délce tropického roku. Protože délka lunace je přibližně 29.5 dne, tak se střídají v roce měsíce o délce 29 a 30 dnů. Díky tomu je rok dlouhý zhruba 354 dnů, ale do přibližné délky tropického roku, chybí 11 dnů. Proto se v cyklu devatenácti let sedmkrát přidává přestupný měsíc a tím se průměrná délka židovského roku zhruba vyrovná délce tropického roku.
Dějiny židovského kalendáře lze rozdělit na tři období: biblické, talmudské a post-talmudské. První období spočívalo čistě na pozorování Slunce a Měsíce, historicky krátké druhé období na pozorování i na výpočtech a třetí už jenom na výpočtech.
Ve starověku nový kalendářní měsíc začínal prvním objevením tenkého srpku Měsíce po novu. Svědkové tohoto úkazu to pak nahlásili do Jeruzaléma, kde se židovská velerada starala o kalendář. Kalendářní rada židovské velerady pak oficiálně vyhlásila "Roš chodeš", začátek nového měsíce. Navíc se před slavností žní pozorovalo, zda jsou již zlaté klasy. Pokud ne, přidal se třináctý měsíc navíc, neboť Hospodin musel dostat za oběť první zlaté klasy. Podrobněji viz stránka Lunisolární cykly, první dva odstavce. Vzdálenějším komunitám se vyhlášení nového měsíce oznamovalo ohňovými signály.
Tehdejší kalendář vycházel z tradice Tóry, z veršů o stvoření světa, které proběhlo takto:
- neděle, 1. den: Bůh stvořil světlo
- pondělí, 2. den: Bůh stvořil nebe
- úterý, 3. den: Bůh stvořil vody, pevniny a na nich rostliny
- středa, 4. den: Bůh stvořil Měsíc, Slunce a hvězdy
- čtvtek, 5. den: Bůh stvořil ryby a ptáky
- pátek, 6. den: Bůh stvořil zvířata co chodí a plazí se. Na konci dne stvořil i člověka
- sobota, 7. den: Vše je hotovo, je den odpočinku
Sobota, židovský šabat, byla dle Tóry poslední ze sedmi dnů stvoření světa. Je to den odpočinku, pro Židy je dodnes celodenní zákaz nejen práce, ale i vaření, manipulace s ohněm a elektronickými přístroji, cestování a podobně. Je to také jediný den v týdnu, který má své vlastní jméno, ostatní dny se jmenují podle pořadí stvoření světa, tedy první den (neděle), druhý den (pondělí) a tak dále až šestého dne což je pátek. Týden začíná nedělí.
Běžný židovský rok má 12 měsíců, původně neměly jména a nazývaly se prostě: první měsíc, druhý měsíc a tak dále. V Tóře jsou zapsány pouze čtyři názvy těchto měsíců: Abib (první měsíc), Ziv (druhý měsíc), Ethanim (sedmý měsíc) a Bul (osmý měsíc). Během babylónského zajetí (6. století př. o. l., zkratka o. l. znamená občanského letopočtu, což je židovské označení našeho křesťanského letopočtu, neboť to není jejich letopočet) Židé převzali babylónská jména měsíců a tak dostaly jednotlivé měsíce svá současná jména. První měsíc je dle Tóry nisan, ten měsíc kdy Židé vyšli z Egypta - je to měsíc zrodu židovského národa. Poslední, dvanáctý měsíc je adar. Pokud je nutné přidat přestupný měsíc, přidává se před tento poslední měsíc.
Avšak již v této době měl kalendář svá pevná pravidla. Novoluní nemohlo nastat dříve, než uplynulo 29½ dne a ⅔ hodiny. Pokud nebylo možné přesně určit měsíc, jeden (plný) měsíc měl 30 dní a následující (krátký) měsíc 29 dní. Přitom plných měsíců mohlo být v roce nejméně 4 a nejvíce 8, takže rok nemohl mít méně než 352 dní a více než 356 dní.
Talmudské období historie kalendáře začalo vyhnáním Židů z Jeruzaléma. Provozovat kalendář jen pomocí vizuálního pozorování srpku Měsíce a následného oznamování ohněm již nebylo možné. Navíc nepřátelští Samaritáni zapalovali dokonce falešné signální ohně a tím zmatek v kalendáři jen narůstal. Rabbi Juda I. (135—217 o. l. proto zrušil ohnivé signály a zaměstnal jízdní posly. Navíc stanovení novoluní podle svědectví svědků ztrácelo na významu a začalo se více spoléhat na astronomické výpočty.
Nakonec rabbi Hillel II. (?—365 o. l.) zavedl v letech 358-9 o. l. pevně stanovený kalendář založený na pouze matematických a astronomických výpočtech. Tím začalo post-talmudské období historie kalendáře. Přestupné roky byly pevně určeny v rámci devatenáctiletého cyklu. Tento cyklus začal rokem 1 a končil rokem 19 a pak se stále periodicky opakuje. Obdobou je zlaté číslo v juliánském a gregoriánském kalendáři. Třináctý měsíc se vkládal ve 3, 6, 8, 11, 14, 17 a 19 roce cyklu. Také byl změně počet plných měsíců v roce, mohlo jich být nejméně 5 a nejvíce 7, takže rok nesměl mít méně než 353 dní a více než 355 dní.
Židovský letopočet se mění až v sedmém měsíci s názvem tišri. I to je pozoruhodná odlišnost od ostatních kalendářů. V běžném životě používá toto číslování měsíců, prvním měsícem je právě tišri a nisan zase sedmým a díky tomu se letopočet mění právě při 1. tišri. Číslování měsíců podle Tóry se nazývá náboženské (biblické) a číslování, kdy se letopočet mění v prvním měsíci, je nazýváno civilní či občanské. Je to podobné jako u nás: rok začíná sice lednem, ale školní rok zářím. Židovský letopočet se často označuje zkratkou AM, což je zkratka latinského Anno Mundi, v překladu doslova 'v roce světa', volněji přeloženo 'od stvoření světa'.
| pořadí | česky | původní babylónské jméno | anglicky | |
|---|---|---|---|---|
| biblické | občanské | |||
| 1 | 7 | nisan | Nisannu | Nisan |
| 2 | 8 | ijar | Airu | Iyar |
| 3 | 9 | sivan | Sivannu | Sivan |
| 4 | 10 | tamuz | Duzu | Tammuz |
| 5 | 11 | av | Abu | Av |
| 6 | 12 | elul | Ululu | Elul |
| 7 | 1 | tišri | Tašritu | Tishrei |
| 8 | 2 | (mar)chešvan | Arach-samna | (Mar)Cheshvan |
| 9 | 3 | kislev | Kisilivu | Kislev |
| 10 | 4 | tevet | Dhabitu | Tevet |
| 11 | 5 | ševat | Sabadhu | Shevat |
| 12 | 6 | adar | Addaru | Adar |
V normálním, nepřestupném roce se pěkně střídá délka měsíců 29 a 30 dnů, adar má 29 dnů. V přestupném roce se před něj vloží měsíc adar I, který je dlouhý 30 dnů. Původní, posunutý měsíc adar se přejmenuje na adar II (šeni - druhý) a má stále 29 dnů.
Židovský rok má tak celkem šest různých délek, po třech pro normální a přestupné roky. Normální nepřestupný rok má 354 dní, počet dnů v jednotlivých měsících je střídavě 30 a 29 dní, měsíc chešvan má 29 dní a kislev 30 dní. Neúplný či také krátký rok má o jeden den méně, 353 dní, měsíce chešvan a kislev mají jen 29 dní. Nadpočetný či také plný rok má zase o jeden den více, 355 dnů, měsíce chešvan a kislev mají 30 dní. Přestupné roky jsou o 30 dnů delší, měsíce chešvan i kislev mají stejný počet dní jako u nepřestupných roků, jen přibyl měsíc Adar I s 30 dny.
| měsíc | počet dnů | |||||
|---|---|---|---|---|---|---|
| tišri | 30 | 30 | 30 | 30 | 30 | 30 |
| chešvan | 29 | 29 | 30 | 29 | 29 | 30 |
| kislev | 29 | 30 | 30 | 29 | 30 | 30 |
| tevet | 29 | 29 | 29 | 29 | 29 | 29 |
| ševat | 30 | 30 | 30 | 30 | 30 | 30 |
| adar, adar I | 29 | 29 | 29 | 30 | 30 | 30 |
| adar II | 29 | 29 | 29 | |||
| nisan | 30 | 30 | 30 | 30 | 30 | 30 |
| ijar | 29 | 29 | 29 | 29 | 29 | 29 |
| sivan | 30 | 30 | 30 | 30 | 30 | 30 |
| tamuz | 29 | 29 | 29 | 29 | 29 | 29 |
| av | 30 | 30 | 30 | 30 | 30 | 30 |
| elul | 29 | 29 | 29 | 29 | 29 | 29 |
| CELKEM v roce | 353 | 354 | 355 | 383 | 384 | 385 |
Židovské svátky
Do židovského náboženského kalendáře se promítla ve formě různých svátků bohatá historie Židů. Zde je stručný přehled těch nejvýznamnějších, všechny svátky se dělí do několika skupin:
| biblické svátky vysoké | Roš hašana, Jom kipur |
| biblické svátky poutní | Pesach, Šavu'ot, Sukot |
| historické svátky | Chanuka, Purim |
| moderní svátky | Jom ha-acma'ut, Jom Jerušalajim |
| postní dny | Půst Gedaljův, 10. tevet, 17. tamuz, Tiš'a be-av |
| ostatní | Roš chodeš, Tu bi-švat, Lag ba-omer, Jom ha-šo'a |
Níže jsou chronologicky setříděné svátky v průběhu celého židovského roku: Mimo Izrael se slaví veškeré svátky kromě Jom kipuru o den déle, je to kvůli židovské diaspoře žijící mimo Izrael. Důvodem je, že ve starověku nebylo možné informovat odlehlé končiny dostatečně rychle o vyhlášení nového měsíce. Po ustanovení pevného kalendáře to již bylo zbytečné, ale tradice slavit po dva dny zůstala zachována. Červeně zvýrazněné svátky jsou zvýrazněny stejným způsobem i ve zdejším židovském ročním kalendáři.
První den v každém měsíci: Roš chodeš
Začátek nového měsíce. Roš chodeš doslova znamená 'hlava měsíce'. Dle Tóry první den měsíce nisan, čtrnáct dní před odchodem Egypta, přikázal Bůh Mojžíši, aby vyhlásil novoluní. Od této chvíle se nepřerušeně vyhlašuje každý začátek nového kalendářního měsíce. Roš chodeš měsíce tišri (kdy začíná nový rok) se neslaví ani neohlašuje, namísto toho se slaví svátek Roš hašana. Více na Wikipedii heslo Roš chodeš.
1. a 2. tišri: Roš hašana
Dle gregoriánského kalendáře je někdy v období září až října. Doslova "hlava roku" - Nový rok, dle židovské tradice je tento svátek chápán jako narozeniny světa. Neodmyslitelným rysem svátku je troubení na beraní roh, zvaný šofar. Více na Wikipedii heslo Roš hašana.
3. tišri: Půst Gedaljův
Veřejný postní den držený na paměť zavraždění místodržícího Gedalji ben Achikam. Gedaljova smrt tak znamenala definitivní konec židovské samostatnosti v Judsku. Dle gregoriánského kalendáře jde měsíce září či říjen. Více na Wikipedii heslo Půst Gedaljův.
10. tišri: Jom kipur
Desátý den po svátku Roš hašana se slaví Jom kipur, Den smíření. Je to den celodenního přísného postu. Dle tradice v tento den odpustil bůh Izraeli zhotovení zlatého telete. V synagogách Židé vyznávají své hříchy, ve svém okolí vyhledávají přátele i nepřátele a prosí o odpuštění. Kdo upřímnou prosbu o odpuštění nepřijme, je pak chápán jako veliký hříšník. Více na Wikipedii heslo Jom kipur.
15.-22. tišri: Sukot
Svátek stánků (chýší, stanů, sklizně) začíná 15. tišri a trvá celý týden, mimo Izrael o den déle, až do 22. tišri. V gregoriánském kalendáři jde o období září až říjen. Tento svátek připomíná odchod z Egypta. V Tóře se píše, že první den odešli Židé z Egypta a utábořili se v místě zvaném Sukot. Více na Wikipedii heslo Sukot.
22. tišri: Šmini aceret
V Izraeli se slaví 22. tišri, mimo něj i 23. tišri. V doslovném překladu je název 'osmý den shromáždění' a navazuje tak na předchozí svátek Sukot. Více na Wikipedii heslo Šmini aceret.
22. tišri: Simchat Tóra
V Izraeli se slaví 22. tišri v tentýž den jako Šmini aceret, mimo Izrael 23. tišri. V synagogách končí roční cyklus čtení Tóry. Více na Wikipedii heslo Simchat Tóra.
25. kislev - 2(3). tevet: Chanuka
Chanuka se slaví osm dní od 25. kislevu do 2. tevetu (v případě že má kislev jen 29 dní, tak do 3. tevetu). Podle gregoriánského kalendáře připadá na období od konce listopadu do konce prosince. Je to oslava na připomínku zázraku z historie židovského národa. Kolem roku 165 př. o. l. Židé osvobodili Jeruzalém a v Chrámu zapálili sedmiramenný svícen, ale měli nedostatek oleje pro něj. Přesto svícen svítil po osm dní, než se vyrobil další olej. Svátek je známý také jako Svátek světel. Zvykem je postupně zapalovat po dnech jednotlivé svíce na osmiramenném svícnu. Více na Wikipedii heslo Chanuka.
Půst 10. tevetu
Veřejný postní den, připomínající počátek obléhání Jeruzaléma babylónským králem Nebukadnesarem II. v roce 588 př. o. l., což byl první krok ke zničení Jeruzaléma, Chrámu a Judského království. Nově se drží půst i za oběti holocaustu. Dle gregoriánského kalendáře jde měsíce prosinec či leden. Více na Wikipedii heslo Půst 10. tevetu.
15. ševat: Tu bi-švat
V kalendářním měsíci ševat začínají v Izraeli kvést první stromy a nastává začátek nového vegetačního cyklu. Proto se mu říká 'Svátek stromů' nebo i 'Slavnost plodů'. Jde o menší svátek, nevztahuje se na něj zákaz práce. Dle gregoriánského kalendáře je svátek v období leden až únor. Více na Wikipedii heslo Tu bi-švat.
14. Adar (II): Purim
Na připomínku záchrany Židů v Perské říši se slaví historický svátek Purim 14. adaru, či v případě přestupného roku, v adaru II. Dle gregoriánského kalendáře připadá na březen. Často je nazýván i jako Svátek losů. Proradný poradce Haman perského krále Achašveroše (cca 5. století př. o. l.) plánoval usmrcení Židů pod záštitou krále. Královna Ester opila krále a přiznala se ke svému židovskému původu. Král na to nechal Hamana popravit a Židé byli zachráněni. Jedna z židovských povinností na tento svátek přikazuje se opít. Dozajista jde tak o oblíbený svátek. Více na Wikipedii heslo Purim.
15.-22. nisan: Pesach
Týden trvající poutní svátek Pesach připomíná vyjití z otroctví v Egyptě a cestu ke svobodě. Jde o jeden z nejstarších svátků a patří mezi nejdůležitější. Dle tóry se má slavit 15. dne prvního měsíce a svátek končí v Izraeli 21. nisanu, mimo Izrael trvá o den déle. Podle gregoriánského kalendář připadá na březen či duben, vlivem nepřesné délky židovského roku vůči tropickému roku je tento svátek v současnosti i měsíc po jarní rovnodennosti a zvolna se posouvá dále. Přitom první dva a poslední dva dny jsou sváteční, při nichž platí podobná pravidla jako při šabatu. Pesach nikdy nezačíná v pondělí, v středu nebo v pátek. Podle Tóry se nesmí po celý svátek Pesach jíst nic kvašeného. To je připomínka rychlého odchodu z Egypta, kdy nebyl čas nechat těsto vykynout. Více na Wikipedii heslo Pesach.
27. nisan: Jom ha-šo'a
Den památky na šoa a hrdinství připomíná šest milionů Židů, kteří byli zavražděni během holokaustu. Podle gregoriánského kalendáře jde o měsíce březen či duben. Více na Wikipedii heslo Jom ha-šo'a.
5. ijar: Jom ha-acma'ut
Den nezávislosti Izraele připomíná vyhlášení nezávislého státu Izrael dne 5. ijaru 5708 (14. května 1948). Podle gregoriánského kalendáře jde měsíce duben a květen. Více na Wikipedii heslo Jom ha-acma'ut.
18. ijar: Lag ba-omer
Jméno v překladu doslova znamená 33. den omeru. Omer je židovský náboženský obřad počítání dnů a týdnů, které uběhly od prvního dne svátku Pesach. Jedná se celkem o 49 dnů, více na Wikipedii heslo Počítání omeru. Vlastní svátek pravděpodobně připomíná den, kdy skončila morová rána, která zabila 24000 žáků rabiho Akivy. Podle gregoriánského kalendáře jde měsíce duben a květen. Více na Wikipedii heslo Lag ba-omer.
28. ijar: Jom Jerušalajim
Den Jeruzaléma je izraelským národním svátkem, jde o připomínku sjednocení Jeruzaléma v průběhu šestidenní války v roce 1967. Dle gregoriánského kalendáře jde měsíce duben či květen. Slaví se od roku 1968. Více na Wikipedii heslo Jom Jerušalajim.
6.-7. sivan: Šavu'ot
Sedm týdnů a jeden den po začátku Pesachu se slaví se 6. sivanu, mimo Izrael i 7. sivanu, další poutní svátek Šavu'ot. Dle gregoriánského kalendář připadá na konec května nebo začátek června. Připomíná den, kdy Hospodin daroval Mojžíšovi Desatero na hoře Sinaj. Více na Wikipedii heslo Šavuot.
Půst 17. tamuzu
Postní den připomínající prolomení jeruzalémských hradeb před zničením Druhého chrámu. Tento den také tradičně připomíná zničení dvou desek Desatera a další historické pohromy, které postihly židovský národ ve stejný den. Dle gregoriánského kalendáře jde měsíce červen či červenec. Více na Wikipedii heslo Půst 17. tamuzu.
9. av: Tiš'a be-av
Postní den připomínající hned několik tragických událostí židovských dějin. Druhého roku po odchodu z Egypta v tento den byli Židé potrestáni čtyřicetiletým putováním na poušti. Zničení Prvního Šalamounova chrámu babylonským králem Nebukadnesarem II. i zničení Druhého chrámu roku Římany. Porážka povstání Bar Kochby proti Římanům. Dle gregoriánského kalendáře jde měsíce červenec či srpen. Více na Wikipedii heslo Tiš'a be-av.
Při pročítání přehledu židovských svátků lze najít jejich analogii v křesťanských svátcích. Není divu, vždyť první křesťané byli Židé a čerpali z židovské tradice. Pesach má svůj protějšek ve Velikonocích, oba jsou na jaře. To je ovšem pochopitelné, ukřižování se odehrálo těsně před Pesachem. Chanuka, kdy se postupně zapaluje osm svící, ma svůj protějšek ve Vánocích, kdy se v průběhu adventu postupně zapalují čtyři svíce. Oba svátky jsou v zimě. Šavu'ot se slaví padesát dní po začátku Pesachu, Hod Boží Svatodušní (dříve Letnice) se také slaví padesát dní po Velikonoční neděli. I Purim, kdy Židé mají karneval, má svůj protějšek a to v masopustu, obě slavnosti jsou na konci zimy.
Pravidla pro výpočty v židovském kalendáři
U židů je i počítání času částečně odlišné od běžně používaného. Židovský den začíná již večer (přesněji jakmile vyjdou tři nejjasnější hvězdy), pro následující výpočty se jako začátek dne bere běžných 18 hodin předchozího dne. V Tóře (prvních pět knih Mojžíšových - základní dokument judaismu) je totiž psáno '…a byl večer a bylo jitro, den první', z čehož lze odvodit, že den začíná večerem. Samotný den se sice dělí také na 24 hodin, ale hodina má 1080 chalakim (v překladu dílků, jednotné číslo je chelek). Jeden chelek je tedy 3⅓ naší sekundy. K odvození vedla následující úvaha: solární rok má zhruba 360 dní a je chápán jako protějšek dne. Protože den má tři části (večer, noc, jitro) tak se i hodina rozdělila na 1080 částí (360×3=1080). Samotný chelek se ještě dělí na 76 ragaím (v překladu okamžik, 0.0438596… sekundy).
V následujícím textu budu často používat základní aritmetické operace s časovými údaji židovského kalendáře. Většinou se pracuje jen se dny týdne, přitom 1=neděle, 2=pondělí a tak dále až do soboty která má číslo 7. Pokud připočítáváme k kalendářnímu datu více dní, pracujeme je s dny, které jsem zbytkem po dělení 7. Například chceme-li připočítat 10 dní, připočítáváme jen 3 - výsledný týdenní den se díky takto upravené délce nemění. Den má zkratku 'd', hodina 'h', chelek 'p' a ragaím 'r', jak je zvykem v anglických odborných textech. Někdy u časových údajů místo číslovky u dne rovnou zobrazím zkratku dne v týdnu, například místo '1d' je 'ne'. U časového intervalu to nemá smysl. Při případném převodu do obvyklých údajů platí, že čas 1d 6h značí ve skutečnosti půlnoc z neděle na pondělí.
Několik příkladů:- 1h 1000p + 81p = 2h 1p
- 1d 23h 800p + 480p = 2d 0h 200p
- 7d 12h + 12h = 1d 0h, lze zapsat i jako 'so 12h + 12h = ne 0h'
- lunace = 29d 12h 793p ≡ 1d 12h 793p, pak
- 12 × lunace = 4d 8h 876p
- 13 × lunace = 5d 21h 589p
- út 9h 204p - 13 × lunace = st 11h 695p
- út 18h 0p + 13 × lunace = po 15h 589p
- út 9h 204p - 12 × lunace = pá 0h 408p
- st 11h 695p + 12 × lunace = ne 20h 491p
Židovský kalendář má pevně stanovené termíny měsíčního novu, přitom jedna lunace trvá přesně 29 dnů 12 hodin a 793 chalakim. Ve dnech je to tedy 29 + 13753 / 25920 = 29.530594 dne. Což je ve srovnání s nynější známou průměrnou délkou lunace 29.530589 dne vynikající přesnost. Při kalendářních výpočtech se tedy nepracuje s přesnými astronomickými údaji!
Svět byl dle židovské tradice stvořen v posledním týdnu roku 1. Na konci šestého dne stvoření světa byl stvořen Adam a ten tak přesně ve 20 hodin (dle židovského počítání dne) spatřil srpek Měsíce. Konjunkce tedy nastala 6 hodin předtím, čili tento první nov tedy nastal v pátek ve 14 hodin. Začátek nového roku určuje nov Měsíce (molad - zrození) kalendářního měsíce tišri v židovském roce. V ten den je svátek "Roš hašana", v překladu doslova hlava roku. Tento molad určil začátek roku 2, předchozí molady jsou extrapolovány. Proto se často píše, že epochou židovského kalendáře je podle juliánského kalendáře den 7. října 3761 př. o. l., kdy v 5 hodin a 204 chalakim dle židovského počítání dne nastal molad. Se dny od půlnoci do půlnoci je to ve skutečnosti 6. října ve 23h 11m 20s. Dle židovského kalendáře to bylo v pondělí prvního dne měsíce tišri roku 1 v 5h 204p. Od tohoto okamžiku běží jednotlivé lunace v pravidelných intervalech a tedy i měsíce židovského kalendáře. Díky vkládání přestupného měsíce se židovské svátky slaví vždy ve stejném ročním období a ve stejný den kalendářního měsíce. Například židovský svátek Sukot, který je v druhé polovině měsíce tišri, je vždy na podzim.
Určení prvního dne roku
Pro zjištění začátku nového židovského roku musíme nejdříve určit, kdy nastává molad pro 1. tišri v daném roce, říkáme mu molad tišri. Nejdříve spočítáme kolik měsíců uběhlo od 1. tišri roku 1, výpočet se provádí jen s celými čísly:
Pak už jen k okamžiku prvního moladu připočteme násobek počtu měsíců s délkou lunace (nepracuje se celými týdny, jen se zbytkem):
Tím dostaneme týdenní den a čas moladu pro 1. tišri daného roku. K přesnému určení dne svátku "Roš hašana" (svátek Nový rok), prvního dne židovského roku, se musí ještě aplikovat čtyři dechijot (pravidla, výjimky, odložení):
- 1. dechijot: židovský Nový rok nesmí navíc připadnou na neděli, středu nebo pátek. Pokud by se tak mělo stát, přesouvá se Nový rok na následující den. Díky tomu, že slavnost Nového roku nemůže být v pátek nebo neděli, nebude slavnost sousedit se sobotou, nebudou tedy dva svátky za sebou. Ale mohou se překrývat, tedy Nový rok může být v sobotu. Ze stejného důvodu nesmí být Nový rok ve středu, neboť by pak důležitý svátek Jom kipur (10. tišri) připadl na pátek a tak by zase byly dva svátky za sebou. Jde o pravidlo ADU. Svátek Nového roku může připadnou jen na týdenní dny s čísly 2, 3, 5 a 7. Dobře se to pamatuje, jde o prvočísla.
- 2. dechijot: pokud molad nastane v 18 hodin židovského času (tedy 12 hodin obvyklého času) nebo později, je jasné, že již nemůže být srpek Měsíce spatřen a Nový rok se přesune na následující den. Jde o pravidlo JACH (nebo Molad Zaken). Může se stát, že se Nový rok přesune na den, který není dovolen. Pak se aplikuje navíc ještě pravidlo ADU a celkový přesun je o dva dny.
- 3. dechijot: pokud molad v nepřestupném roce nastane v úterý v 9 hodin 204 chalakim židovského času nebo později, přesouvá se Nový rok hned o dva dny, neboť podle předchozího pravidla nemůže být ve středu. Bez posunu by totiž molad tišri následujícího roku (12 moladů trvá 354d 8h 876p, bez celých týdnů to je 4d 8h 876p) připadl na sobotu po 18 hodině (3d 9h 204p + 4d 8h 876p = 7h 18h 0p), takže podle pravidel 1 a 2 by se příští Roš hašana odložila až na pondělí a rok by pak měl délku 356 dnů, což není dovoleno. Toto dechijot zajišťuje, že jich bude mít pouze 354. Jde o dechijot GATARAD (nebo zřídka 356 Rule).
- 4. dechijot: pokud byl předchozí rok přestupný (13 moladů trvá 383d 21h 589p, bez celých týdnů to je 5d 21h 589p) a molad nastává v pondělí v 15 hodin 589 chalakim či později, přesouvá se Nový rok na úterý. Bez posunu by totiž molad tišri předchozího přestupného roku totiž připadl na úterý po 18 hodině, takže podle pravidel 1 a 2 byl předchozí Roš hašana odložen na čtvrtek (2d 15h 589p - 5d 21h 589p = 3d 18h 0p). A pokud by přestupný rok trval od čtvrtka do neděle, měl by jen 382 dnů a to také není dovoleno. Toto pravidlo zase zajišťuje, že předchozí přestupný rok bude od čtvrtka do pondělí a bude mít délku 383 dnů. Jde o řídce používané dechijot s názvem BETUTAKPAT (nebo také zřídka 382 Rule).
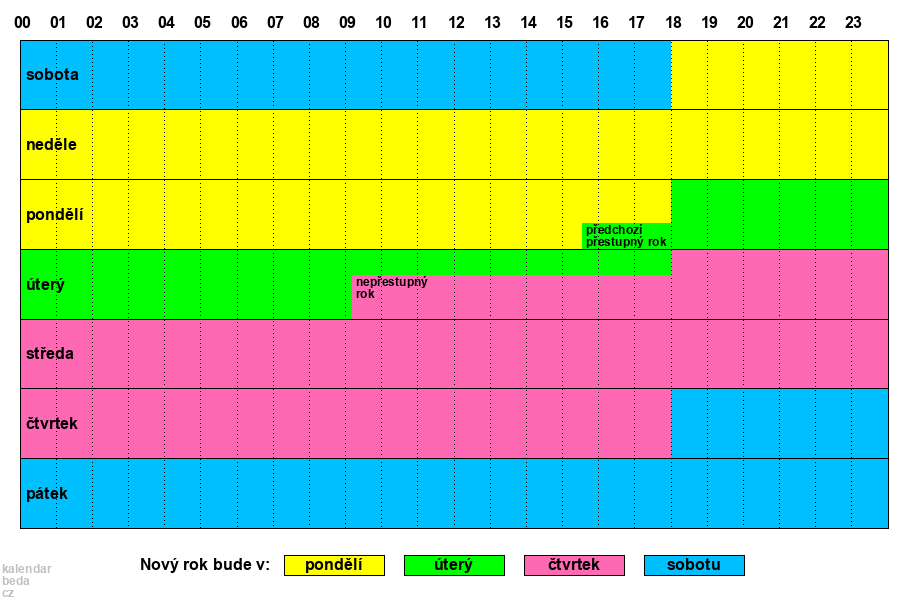
Na níže zobrazené grafu je aplikace těchto čtyř dechijot graficky. Najdete si jen den týdne v řádku, pak čas moladu ve sloupci a dle barvy určíte den 1. tišti, slavnost Nového roku. Pozor na výjimky pro 3. a 4. dechijot, zde je ještě nutné rozhodnout, zda-li splňují dodatečné podmínky.
Nyní si lehce můžeme vypočítat četnost dne týdne pro Nový rok. Vlastně počítáme plochu vybrané barvy, tedy dne pro Nový rok. Pro sobotu je to patrné v grafu na první pohled, zabere přesně dva dny ze sedmi.
Pondělí také zabírá dva dny, ale ještě nutno odečíst posuny po provedení dechijot BETUTAKPAT. Tento dechijot se použije jen pro předcházející přestupné roky, těch je 7 v cyklu 19 let. A jen v čase od 15h 589p do 18h 0p, to je doba dlouhá 2651p. Celý týden trvá 7×24×1080 = 181440p.
Úterý zabírá pouze jeden den, ale je nutné připočítat posuny po provedeni dechijot BETUTAKPAT a odečíst posuny kvůli dechijot GATARAD. Dechijot GATARAD se použije jen v nepřestupných letech, těch je 12 v cyklu 19 let. A navíc jen od 9h 204p do 18h 0p, to je doba dlouhá 9516p. Celý týden trvá 7×24×1080 = 181440p.
Čtvrtek zabírá dva dny a ještě navíc posuny po provedení dechijot GATARAD:
Obdobně si můžeme z grafu určit pravděpodobnosti použití určité dechijot. U prvního dechijot ADU je to jednoduché, týká se tří dnů ze sedmi (neděle, středa a pátek), pravděpodobnost je tedy:
Druhé dechijot JACH a to včetně kombinace JACH+ADU se použije v poslední čtvrtině dne ve zbývajících čtyřech dnech:
Toto číslo ještě rozdělíme na samotné dechijot JACH, které se použije jen v poslední čtvrtině pondělí:
A zbytek je pak použití kombinace dechijot JACH+ADU:
Třetí dechijot GATARAD se použije jen v nepřestupných letech, těch je 12 v cyklu 19 let. A navíc jen od 9h 204p do 18h 0p, to je doba dlouhá 9516p. Celý týden trvá 7×24×1080 = 181440p.
A nakonec čtvrté dechijot BETUTAKPAT se použije jen pro předcházející přestupné roky, těch je 7 v cyklu 19 let. A jen v čase od 15h 589p do 18h 0p, to je doba dlouhá 2651p.
Ve zbývajících 39% se žádné pravidlo nepoužije.
Keviah: typ roku
Jako jsou nedělní písmena juliánského i gregoriánského kalendáře, tak jejich obdobou je v židovském kalendáři keviah (množné číslo keviot), který také udává typ roku. V originále je vše pochopitelně hebrejsky, ale my se spokojíme s anglickým značením.
Jak už víme židovský rok má celkem šest různých délek, po třech pro normální a přestupné roky, každý druh má své jméno. Normální nepřestupný rok má 354 dní, často se označuje písmenem r (z anglického regular). Neúplný či také krátký rok má o jeden den méně, 353 dní, označuje se písmenem d (deficient). Nadpočetný či také plný rok má zase o jeden den více, 355 dnů a značí se a (abudant) nebo c (complet, zde však nepoužívám). Přestupné roky jsou o 30 dnů delší, mají stejná jména a označují se stejnými písmeny, ale velkými (R, D, A). V odborné literatuře však existují i jiná označení typů roků, původní označení je ovšem hebrejské.
Keviah (typ roku) má dva znaky. Na prvním místě je pořadové číslo dne v týdnu (přitom 1=neděle, 2=pondělí,… 7=sobota) pro 1. tišri a pak označení délky roku. Často se používá i třetí znak, který udává pořadové číslo dne v týdnu pro 15. nisan (díky tomu se rozeznají přestupné roky, které se pak nemusí lišit velikostí písmen). Ovšem dvouznakové značení je nejkompaktnější, například 3R značí přestupný rok, dlouhý 384 dní, který začíná v úterý.
Rok může začínat pouze v pondělí, úterý, čtvrtek a v sobotu. Existuje 6 délek roků, což dává celkem 24 možností. Některé kombinace můžeme vyškrtnout, neb při nevhodné délce roku by příští rok začínal v zakázaný týdenní den. Zbude 15 možností, jedna z nich je, že přestupný rok začíná v úterý (jeho molad je před út 18h) a trvá 385 dnů, končí tedy v pondělí. To znamená, že příští, nepřestupný rok by měl začínat v úterý. Molad tišri tohoto příštího roku je ale určitě před 15h 589p v pondělí (út 18h + 5d 21h 589p = po 15h 589p) a nemůže se tak použít pravidlo BETUTAKPAT (posunutí začátku roku o jeden den) na tento příští rok, čili délka předcházejícího přestupného roku nikdy nebude prodloužena o den na 385 dnů. Pokud přestupný rok začíná v úterý, nikdy nemůže mít délku 385 dní. Takže z 24 kombinací začátku roku a jeho délky, zbude jen 14 reálných typů ročního kalendáře. To je shodou okolností stejné číslo jako počet typů ročního gregoriánského (i juliánského) kalendáře vyjma velikonočních dat.
| délka roku | začátek roku | |||
|---|---|---|---|---|
| pondělí | úterý | čtvrtek | sobota | |
| 353 | 2d | 7d | ||
| 354 | 3r | 5r | ||
| 355 | 2a | 5a | 7a | |
| 383 | 2D | 5D | 7D | |
| 384 | 3R | |||
| 385 | 2A | 5A | 7A | |
Jakmile známe délku roku, známe i délky jednotlivých kalendářních měsíců v roce. Pak již není třeba počítat molady pro tyto měsíce, průměrná délka měsíců ve dnech dobře aproximuje délku lunace. Příklad pro reálné roky je na stránce Přesnost moladu, kde se porovnává rozdíl mezi moladem pro daný měsíc a nejbližším astronomickým novem.
Čtyři brány židovského kalendáře
Nejjednodušší metoda pro zjištění typu roku (kevia) je vypočítat den 1. tišri dvou po sobě jdoucích let. Odečtením pak zjistíme délku roku. Přesto je možné jen z moladu tišri a z pozice roku v devatenáctiletém cyklu určit jeho typ. Jde to pomocí tabulky čtyř bran, jejíž sestavení představuje vrchol znalostí pravidel židovského kalendáře. Jde o babylonský vynález z 9. století. Roky se v devatenáctiletém cyklu rozdělí do čtyř skupin:
- roky následující po přestupném roce, ale nepředcházející přestupnému roku: 1, 4, 9, 12 a 15
- roky mezi dvěma přestupnými roky: 7 a 18
- roky předcházející přestupnému roku, ale nenásledující po něm: 2, 5, 10, 13 a 16
- přestupné roky: 3, 6, 8, 11, 14, 17 a 19
Tyto skupiny tvoří čtyři sloupce v tabulce. Řádky pak tvoří meze pro molad tišri. Na průsečíku pak nalezneme hledaný typ roku. Například molad tišri pro rok 5788 nastane v pátek 0h 572p. Najdeme řádek s tímto údajem nebo nejbližší předcházejícím hodnotou, v tomto případě jde o řádek 'pá 0h 408p'. Rok 5788 je v devatenáctiletém cyklu dvanáctý v pořadí. Na průsečíku se sloupcem, kde je 12, nalezneme typ roku 7a. Rok 5788 tedy začíná v sobotu a má délku 355 dnů.
| molad tišri | roky v devatenáctiletém cyklu | |||
|---|---|---|---|---|
| roky následující po přestupném roce, ale nepředcházející přestupnému roku | roky mezi dvěma přestupnými roky | roky předcházející přestupnému roku, ale nenásledující po něm | přestupné roky | |
| 1 4 9 12 15 | 7 18 | 2 5 10 13 16 | 3 6 8 11 14 17 19 | |
| so 18h 0p | 2d(po,353) | 2D(po,383) | ||
| ne 9h 204p | 2a(po,355) | |||
| ne 20h 491p | 2A(po,385) | |||
| po 15h 589p | 3r(út,354) | |||
| po 18h 0p | 3R(út,384) | |||
| út 9h 204p | 5r(čt,354) | |||
| út 18h 0p | 5D(čt,383) | |||
| st 11h 695p | 5A(čt,385) | |||
| čt 9h 204p | 5a(čt,355) | |||
| čt 18h 0p | 7d(so,353) | 7D(so,383) | ||
| pá 0h 408p | ||||
| pá 9h 204p | 7a(so,355) | |||
| pá 20h 491p | 7A(so,385) | |||
Tekufy: roční doby
Podivně jsou v židovském kalendáři řešeny roční doby (tekufy), s přesně určenými astronomickými jevy (slunovrat, rovnodennost) nemají nic společného. Tekufa nenese název roční doby, ale kalendářního měsíce ve kterém se nejčastěji vyskytuje. Podle prastaré židovské pověry se nesmí pít voda, která byla v domě hodinu po začátku nové roční doby, neboť je otrávena. Výpočet začátky tekufy je řešen na podobném principu jako počítání měsíčních fází. Tedy je určeno datum první tekufy a její pevná délka, která je čtvrtinou dané délky roku, nebere se tedy ohled na nestejně dlouhé skutečné roční doby. Pak od data první tekufy běží v pravidelných intervalech další tekufy. Přitom platí pravidlo, že první den svátku Pesach (15. nisan) nesmí být dříve než v den jarní rovnodennosti (tekufa nisan) (porovnejte s křesťanským požadavkem, aby Velikonoční neděle byla po začátku jara).
| tekufa | astronomický ekvivalent | začíná | čas |
|---|---|---|---|
| nisan | jarní rovnodennost | jaro | čas semen |
| tamuz | letní slunovrat | léto | doba slizně |
| tišri | podzimní rovnodennost | podzim | čas vinobraní |
| tevet | zimní slunovrat | zima | zimní čas |
Existují dokonce dva systémy pro výpočet, liší se jen prvním kalendářním datem a délkou tekufy. Samuelovská tekufa (pojmenována dle židovského učence Samuela z Nehardy) má jako výchozí datum 22. adar 0 hodin roku 1 a délka tekufy je 91 dnů 7 hodin a 540 chalakim (což je přesně jedna čtvrtina délky roku 365 dnů a 6 hodin - to je délka juliánského roku). Určení výchozího data vychází z tradice, že Slunce bylo vytvořeno na začátku čtvrtého dne stvoření a to začínal 27. elul roku 1. Za 15 hodin pak nastala podzimní rovnodennost. Odečteme-li od tohoto okamžiku délku dvou tekuf dostaneme 22. adar 0 hodin
Addovská tekufa (pojmenována dle židovského učence Adda bar Ahavah) má jako výchozí datum jiné, je jím 29. adar 0 hodin roku 1. Čerpá totiž z jiné tradice, kdy svět byl stvořen v týdnu, kdy končil měsíc adar a začínal nisan roku 1. Právě na začátku čtvrtého dne stvoření (29. adar) bylo stvořeno Slunce a bylo to v okamžik jarní rovnodennosti. Délka roku je vypočtena z 19letého cyklu, kdy se vystřídá 235 moladů. Z toho plyne délka roku 365 dní 5 hodin 997 chalakim a 48 ragaím, což je 365.2468222 dne, tedy ani zde není přesnost délky roku velká. Čtvrtinou z této délky je potom tekufa dlouhá 91 dnů 7 hodin 519 chalakim a 31 ragaím. Časová jednotka ragaím je právě navržena tak, aby tato délka byla právě na celé ragaímy, bez zlomků (ragaím je 1/76 cheleku, 76 = 4 × 19).
Ne vždy podaří dodržet pravidlo, že první den svátku Pesach nesmí být dříve než v den jarní rovnodennosti, ale méně konfliktů dává méně používaná addovská tekufa. Protože cyklus tekuf obou systémů běží nezávisle na cyklu moladů, výsledkem je, že ojediněle jsou v jednom židovském roce jen tři tekufy či, v případě přestupného roku, zase pět tekuf. Navíc se v průběhu tisíciletí vlivem nepřesné délky roku tekufy posunou do jiných ročních dob.
Cykly židovského kalendáře
V židovském kalendáři existují dva hlavní cykly: machzor gadol (velký cyklus) o dvaceti osmi slunečních letech a machzor katan (malý cyklus, nám dobře známý metonův cyklus) o devatenácti lunárních letech. V osmadvaceti slunečních letech se samuelovská tekufa vrací do stejných týdenních dnů a hodin. Na počátku tohoto cyklu se koná židovský obřad Birkat HaHamah (Požehnání Slunce). Naposledy se tak stalo v židovském roce 5769 ve středu 14. nisanu (8. dubna 2009) a příště se tak stane o 28 let později, tedy v roce 5797 opět ve středu 23. nisanu (8. dubna 2037). Cyklus devatenácti lunárních let se sedmi měsíci navíc v sedmi přestupných letech se přibližně rovná devatenácti slunečním rokům, rozdíl je jen jeden a půl hodiny. Cyklus 13 devatenáctiletých cyklů, tedy 247 let, se nazývá iggul, po této době se s drobným rozdílem začínají opakovat časy moladů ve stejné týdenní dny. Ve středověku si dokonce někteří učenci mysleli, že právě po této době se začnou opakovat kalendářní data ve stejném pořadí v židovském kalendáři.
Každý rok dělitelný beze zbytku 7 je sabatickým rokem sedmiletého zemědělského cyklu, rokem šmity, kdy podle židovského náboženského práva halachy musí země ležet ladem. Platí to však pouze pro Izrael, kde se půda nesmí obdělávat ani sklízet a pokud na ní něco přece jen vyroste, smí si plody vzít kdokoli, především však chudí. Ovšem většina farmářů rok šmity obchází různými kličkami.
Periodou kalendáře se rozumí doba, kdy se začnou opakovat kalendářní data ve stejném pořadí. V případě tohoto kalendáře hledáme dobu, kdy se molad tišri zase vrátí přesně ke své hodnotě, včetně týdenního dne. Pak se zase vše opakuje. Jeden molad trvá 29d 12h 793p, bez celých týdnů je to 1d 12h 793p. Celý 19-letý cyklus má 235 moladů, to je opět bez celých týdnů 2d 16h 595p, to jest 69715p. Jeden týden má samozřejmě 7d, tedy 181440p. A nyní hledáme přirozená čísla pro něž platí:
nejmenší společný dělitel obou čísel je 5, výraz lze zkrátit na:
13943 × N = 36288 × M
Jde o nesoudělná čísla, nejmenším řešením pro N je tedy právě 36288. Tolik musí proběhnout 19-letých cyklů, aby se kalendářní data v židovském kalendáři opakovala ve stejném pořadí. Perioda židovského kalendáře je tedy 689472 let, to je 251827457 dní (pozor, jednotlivé 19-leté cykly mají různou délku, viz níže), průměrná délka roku tak vychází na 365.2468222 dne. To není nejlepší přesnost, k chybě jednoho dne dojde už za 216 let.
Trochu statistiky pro celou periodu židovského kalendáře délky 689472 let. Četnost jednotlivých možných délek roků po aplikaci dechijot v celé periodě. Procenta ve sloupci 'celkem' srovnejte s teoretickými hodnotami vypočtenými pod obrázkem Aplikace dechijot v grafu.
| dechijot | délka roku | kolikrát | celkem |
|---|---|---|---|
| nic | 354 | 47634 | 39.01% 268937 |
| 355 | 112439 | ||
| 384 | 27216 | ||
| 385 | 81648 | ||
| ADU | 353 | 38118 | 42.86% 295488 |
| 354 | 62208 | ||
| 355 | 86298 | ||
| 383 | 79461 | ||
| 385 | 29403 | ||
| JACH-ADU | 353 | 31104 | 10.71% 73872 |
| 354 | 15552 | ||
| 383 | 27216 | ||
| JACH | 354 | 15552 | 3.57% 24624 |
| 384 | 9072 | ||
| GATARAD | 354 | 22839 | 3.31% 22839 |
| BETUTAKPAT | 354 | 3712 | 0.54% 3712 |
Statistika pro odložení Nového roku v celé periodě:
- žádné odložení: 268937×
- o jeden den: 323824×
- o dva dny: 96711×
Statistika pro všechny typy roků, včetně poměrného zastoupení v celé periodě. Nejčastějším rokem je rok typu 5r, který se vyskytuje v skoro v pětině všech roků. Nejméně častým rokem je zase rok typu 5a, který se vyskytuje v pouhé třicetině všech roků: Délka 355 dnů je zase nejčastější délka roku.
| délka roku | začátek roku | celkem | |||
|---|---|---|---|---|---|
| pondělí | úterý | čtvrtek | sobota | ||
| 353 | 2d:5.71% 39369 | 7d:4.33% 29853 | 10.04% 69222 | ||
| 354 | 3r:6.25% 43081 | 5r:18.05% 124416 | 24.29% 167497 | ||
| 355 | 2a:11.8% 81335 | 5a:3.31% 22839 | 7a:13.72% 94563 | 28.82% 198737 | |
| 383 | 2D:5.8% 40000 | 5D:3.87% 26677 | 7D:5.8% 40000 | 15.47% 106677 | |
| 384 | 3R:5.26% 36288 | 5.26% 36288 | |||
| 385 | 2A:4.72% 32576 | 5A:6.66% 45899 | 7A:4.72% 32576 | 16.11% 111051 | |
| CELKEM | 28.03% 193280 | 11.51% 79369 | 31.88% 219831 | 28.57% 196992 | 100.00% 689472 |
Další tabulka zobrazuje četnost typů roku pro dané pořadí v devatenáctiletém cyklu:
| # | 2d | 7d | 3r | 5r | 2a | 5a | 7a | 2D | 5D | 7D | 3R | 2A | 5A | 7A | celkem |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3280 | 1377 | 3811 | 10368 | 6557 | 1904 | 8991 | 36288 | |||||||
| 2 | 3281 | 3281 | 3281 | 10368 | 7087 | 1903 | 7087 | 36288 | |||||||
| 3 | 5714 | 3811 | 5714 | 5184 | 4654 | 6557 | 4654 | 36288 | |||||||
| 4 | 3281 | 1378 | 3811 | 10368 | 6557 | 1903 | 8990 | 36288 | |||||||
| 5 | 3281 | 3281 | 3281 | 10368 | 7087 | 1903 | 7087 | 36288 | |||||||
| 6 | 5714 | 3811 | 5714 | 5184 | 4654 | 6557 | 4654 | 36288 | |||||||
| 7 | 3281 | 3281 | 3811 | 10368 | 6557 | 1903 | 7087 | 36288 | |||||||
| 8 | 5714 | 3811 | 5714 | 5184 | 4654 | 6557 | 4654 | 36288 | |||||||
| 9 | 3281 | 1378 | 3811 | 10368 | 6557 | 1903 | 8990 | 36288 | |||||||
| 10 | 3281 | 3281 | 3281 | 10368 | 7087 | 1903 | 7087 | 36288 | |||||||
| 11 | 5714 | 3811 | 5714 | 5184 | 4654 | 6557 | 4654 | 36288 | |||||||
| 12 | 3281 | 1378 | 3811 | 10368 | 6557 | 1903 | 8990 | 36288 | |||||||
| 13 | 3281 | 3281 | 3281 | 10368 | 7087 | 1903 | 7087 | 36288 | |||||||
| 14 | 5714 | 3811 | 5714 | 5184 | 4654 | 6557 | 4654 | 36288 | |||||||
| 15 | 3281 | 1377 | 3811 | 10368 | 6557 | 1903 | 8991 | 36288 | |||||||
| 16 | 3280 | 3280 | 3280 | 10368 | 7088 | 1904 | 7088 | 36288 | |||||||
| 17 | 5715 | 3811 | 5715 | 5184 | 4653 | 6557 | 4653 | 36288 | |||||||
| 18 | 3280 | 3280 | 3811 | 10368 | 6557 | 1904 | 7088 | 36288 | |||||||
| 19 | 5715 | 3811 | 5715 | 5184 | 4653 | 6557 | 4653 | 36288 | |||||||
| CELKEM | 39369 | 29853 | 43081 | 124416 | 81335 | 22839 | 94563 | 40000 | 26677 | 40000 | 36288 | 32576 | 45899 | 32576 | 689472 |
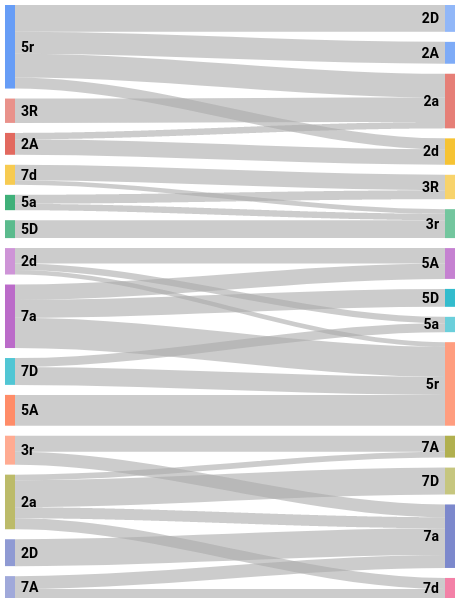
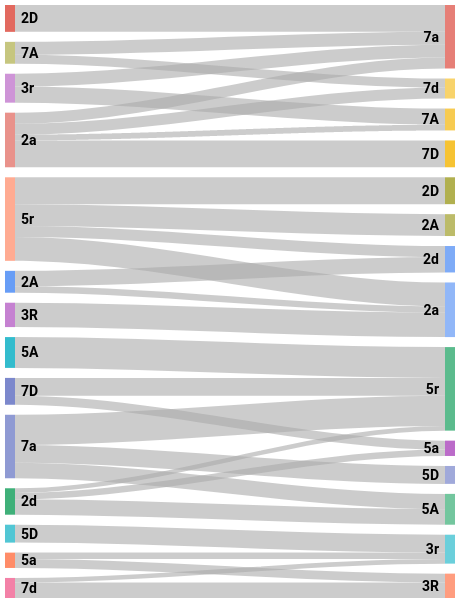
Je zřejmé, že na příklad po přestupném roce následuje vždy jen nepřestupný rok. Prostě po vybraném typu roku mohou následovat jen určité typy. A naopak, vybraný typ roku předchází jen některý typy. Můžeme si ukázat tabulky a grafy, která zobrazují, jaké typy roků předcházejí a následují danému typu roku a kolikrát toto nastane v celé periodě:
| předcházející možné typy | typ |
|---|---|
| 5r:32576 | 2A |
| 5r:40000 | 2D |
| 2A:9611 | 2a |
| 5r:35436 | |
| 3R:36288 | |
| 2A:22965 | 2d |
| 5r:16404 | |
| 7d:22965 | 3R |
| 5a:13323 | |
| 5D:26677 | 3r |
| 5a:9516 | |
| 7d:6888 | |
| 7a:22934 | 5A |
| 2d:22965 | |
| 7a:26677 | 5D |
| 7D:13323 | 5a |
| 2d:9516 | |
| 5A:45899 | 5r |
| 7a:44952 | |
| 2d:6888 | |
| 7D:26677 | |
| 3r:24026 | 7A |
| 2a:8550 | |
| 2a:40000 | 7D |
| 2a:16381 | 7a |
| 3r:19055 | |
| 2D:40000 | |
| 7A:19127 | |
| 7A:13449 | 7d |
| 2a:16404 |
| typ | následující možné typy |
|---|---|
| 2A | 2d:22965 |
| 2a:9611 | |
| 2D | 7a:40000 |
| 2a | 7a:16381 |
| 7D:40000 | |
| 7A:8550 | |
| 7d:16404 | |
| 2d | 5r:6888 |
| 5A:22965 | |
| 5a:9516 | |
| 3R | 2a:36288 |
| 3r | 7a:19055 |
| 7A:24026 | |
| 5A | 5r:45899 |
| 5D | 3r:26677 |
| 5a | 3r:9516 |
| 3R:13323 | |
| 5r | 2D:40000 |
| 2A:32576 | |
| 2a:35436 | |
| 2d:16404 | |
| 7A | 7d:13449 |
| 7a:19127 | |
| 7D | 5r:26677 |
| 5a:13323 | |
| 7a | 5D:26677 |
| 5A:22934 | |
| 5r:44952 | |
| 7d | 3R:22965 |
| 3r:6888 |
Pokud rozdělíme všechny roky v celé periodě židovského kalendáře do cyklů po devatenácti letech, dostaneme jen 61 různých sérií typů (keviot) roků. V níže uvedené tabulce je v prvním sloupci pořadové číslo série, v odborné literatuře je to nejčastější číslování, existují však i jiná. V druhém sloupci jsou vypsány za sebou typy všech devatenácti roků série. Třetí sloupec udává délku série ve dnech. Vidíme, že jednotlivé série devatenáctiletých cyklů jsou i různě dlouhé. Rozmezí délek se pohybuje mezi 6939 dny až 6942 dny. Přitom série číslo 61 je ojedinělá, má jako jediná největší délku 6942 dnů. Ve čtvrtém sloupci je nejdřívější možný molad tišri prvního roku série. Celá série má pak také nejpozdější možný molad tišri téhož roku. Jakmile se tato mez překročena, změní se i celá série. Například 1. série může začít nejdříve v sobotu 18h 0p a nejpozději v tentýž den 18h 22p (o jeden chelek méně než je začátek následující série). Tato série tedy zabere celkem krátký interval 22 chalakim z celého týdne. Proto i její četnost v celé periodě židovského kalendáře je malá. Tato četnost je uvedena v pátém sloupci. Je jasné, že poměr intervalu začátku série ku délce týdne (181440p) a poměr četnosti série ku počtu devatenáctiletých cyklů v periodě kalendáře (36288) se rovnají.
| číslo série | typy všech 19 roků v sérii | délka série ve dnech | nejdřívější možný molad 1. roku | počet |
|---|---|---|---|---|
| 01 | 2d5r2A2d5a3R2a7D5r2a7A7d3r7A7a5r2D7a5A | 6940 | so 18h 0p | 4 |
| 02 | 2d5r2A2a7d3R2a7D5r2a7A7d3r7A7a5r2D7a5A | 6940 | so 18h 23p | 535 |
| 03 | 2d5r2A2a7d3R2a7D5a3r7A7d3r7A7a5r2D7a5A | 6940 | so 20h 537p | 5 |
| 04 | 2d5r2A2a7d3R2a7D5a3r7A7a5r2D7a5r2D7a5A | 6940 | so 20h 560p | 833 |
| 05 | 2d5a3R2a7d3R2a7D5a3r7A7a5r2D7a5r2D7a5A | 6940 | ne 0h 408p | 1065 |
| 06 | 2d5a3R2a7d3R2a7A7d3r7A7a5r2D7a5r2D7a5A | 6940 | ne 5h 333p | 540 |
| 07 | 2d5a3R2a7d3R2a7A7d3r7A7a5r2D7a5r2A2d5A | 6940 | ne 7h 870p | 298 |
| 08 | 2a7d3R2a7d3R2a7A7d3r7A7a5r2D7a5r2A2d5A | 6940 | ne 9h 204p | 5 |
| 09 | 2a7d3R2a7a5D3r7A7d3r7A7a5r2D7a5r2A2d5A | 6940 | ne 9h 227p | 535 |
| 10 | 2a7d3R2a7a5D3r7A7a5r2D7a5r2D7a5r2A2d5A | 6940 | ne 11h 741p | 2438 |
| 11 | 2a7d3R2a7a5D3r7A7a5r2D7a5r2A2d5r2A2d5A | 6940 | ne 22h 1051p | 4 |
| 12 | 2a7d3R2a7a5D3r7A7a5r2D7a5r2A2d5r2A2a7D | 6940 | ne 22h 1074p | 299 |
| 13 | 2a7a5D3r7a5D3r7A7a5r2D7a5r2A2d5r2A2a7D | 6940 | po 0h 408p | 535 |
| 14 | 2a7a5D3r7a5A5r2D7a5r2D7a5r2A2d5r2A2a7D | 6940 | po 2h 922p | 539 |
| 15 | 2a7a5D3r7a5A5r2D7a5r2D7a5r2A2d5a3R2a7D | 6940 | po 5h 379p | 1899 |
| 16 | 2a7a5D3r7a5A5r2D7a5r2A2d5r2A2d5a3R2a7D | 6940 | po 14h 152p | 5 |
| 17 | 2a7a5D3r7a5A5r2D7a5r2A2d5r2A2a7d3R2a7D | 6940 | po 14h 175p | 298 |
| 18 | 3r7a5D3r7a5A5r2D7a5r2A2d5r2A2a7d3R2a7D | 6939 | po 15h 589p | 535 |
| 19 | 3r7a5A5r2d5A5r2D7a5r2A2d5r2A2a7d3R2a7D | 6939 | po 18h 23p | 540 |
| 20 | 3r7a5A5r2d5A5r2D7a5r2A2d5a3R2a7d3R2a7D | 6939 | po 20h 560p | 1065 |
| 21 | 3r7a5A5r2d5A5r2D7a5r2A2d5a3R2a7d3R2a7A | 6941 | út 1h 485p | 833 |
| 22 | 3r7a5A5r2d5A5r2A2d5r2A2d5a3R2a7d3R2a7A | 6941 | út 5h 333p | 5 |
| 23 | 3r7a5A5r2d5A5r2A2d5r2A2a7d3R2a7d3R2a7A | 6941 | út 5h 356p | 4 |
| 24 | 3r7a5A5r2d5A5r2A2d5r2A2a7d3R2a7a5D3r7A | 6941 | út 5h 379p | 829 |
| 25 | 5r2d5A5r2d5A5r2A2d5r2A2a7d3R2a7a5D3r7A | 6939 | út 9h 204p | 5 |
| 26 | 5r2d5A5r2a7D5r2A2d5r2A2a7d3R2a7a5D3r7A | 6939 | út 9h 227p | 535 |
| 27 | 5r2d5A5r2a7D5r2A2d5a3R2a7d3R2a7a5D3r7A | 6939 | út 11h 741p | 1903 |
| 28 | 5r2d5A5r2a7D5r2A2a7d3R2a7d3R2a7a5D3r7A | 6939 | út 20h 537p | 5 |
| 29 | 5r2d5A5r2a7D5r2A2a7d3R2a7a5D3r7a5D3r7A | 6939 | út 20h 560p | 534 |
| 30 | 5r2d5A5r2a7D5r2A2a7d3R2a7a5D3r7a5A5r2D | 6939 | út 22h 1074p | 299 |
| 31 | 5r2a7D5r2a7D5r2A2a7d3R2a7a5D3r7a5A5r2D | 6939 | st 0h 408p | 535 |
| 32 | 5r2a7D5r2a7D5a3R2a7d3R2a7a5D3r7a5A5r2D | 6939 | st 2h 922p | 1903 |
| 33 | 5r2a7D5r2a7A7d3R2a7d3R2a7a5D3r7a5A5r2D | 6939 | st 11h 718p | 5 |
| 34 | 5r2a7D5r2a7A7d3R2a7a5D3r7a5D3r7a5A5r2D | 6939 | st 11h 741p | 535 |
| 35 | 5r2a7D5r2a7A7d3R2a7a5D3r7a5A5r2d5A5r2D | 6939 | st 14h 175p | 833 |
| 36 | 5r2a7D5a3r7A7d3R2a7a5D3r7a5A5r2d5A5r2D | 6939 | st 18h 23p | 1605 |
| 37 | 5r2a7D5a3r7A7d3R2a7a5D3r7a5A5r2d5A5r2A | 6941 | čt 1h 485p | 298 |
| 38 | 5r2a7A7d3r7A7d3R2a7a5D3r7a5A5r2d5A5r2A | 6941 | čt 2h 899p | 5 |
| 39 | 5r2a7A7d3r7A7a5D3r7a5D3r7a5A5r2d5A5r2A | 6941 | čt 2h 922p | 535 |
| 40 | 5r2a7A7d3r7A7a5D3r7a5A5r2d5A5r2d5A5r2A | 6941 | čt 5h 356p | 4 |
| 41 | 5r2a7A7d3r7A7a5D3r7a5A5r2d5A5r2a7D5r2A | 6941 | čt 5h 379p | 829 |
| 42 | 5a3r7A7d3r7A7a5D3r7a5A5r2d5A5r2a7D5r2A | 6941 | čt 9h 204p | 5 |
| 43 | 5a3r7A7a5r2D7a5D3r7a5A5r2d5A5r2a7D5r2A | 6941 | čt 9h 227p | 1899 |
| 44 | 7d3r7A7a5r2D7a5D3r7a5A5r2d5A5r2a7D5r2A | 6939 | čt 18h 0p | 539 |
| 45 | 7d3r7A7a5r2D7a5A5r2d5A5r2d5A5r2a7D5r2A | 6939 | čt 20h 537p | 5 |
| 46 | 7d3r7A7a5r2D7a5A5r2d5A5r2a7D5r2a7D5r2A | 6939 | čt 20h 560p | 534 |
| 47 | 7d3r7A7a5r2D7a5A5r2d5A5r2a7D5r2a7D5a3R | 6939 | čt 22h 1074p | 299 |
| 48 | 7a5r2D7a5r2D7a5A5r2d5A5r2a7D5r2a7D5a3R | 6939 | pá 0h 408p | 1605 |
| 49 | 7a5r2D7a5r2D7a5A5r2d5A5r2a7D5r2a7A7d3R | 6939 | pá 7h 870p | 833 |
| 50 | 7a5r2D7a5r2A2d5A5r2d5A5r2a7D5r2a7A7d3R | 6939 | pá 11h 718p | 5 |
| 51 | 7a5r2D7a5r2A2d5A5r2a7D5r2a7D5r2a7A7d3R | 6939 | pá 11h 741p | 535 |
| 52 | 7a5r2D7a5r2A2d5A5r2a7D5r2a7D5a3r7A7d3R | 6939 | pá 14h 175p | 1903 |
| 53 | 7a5r2D7a5r2A2d5A5r2a7D5r2a7A7d3r7A7d3R | 6939 | pá 22h 1051p | 4 |
| 54 | 7a5r2D7a5r2A2d5A5r2a7D5r2a7A7d3r7A7a5D | 6940 | pá 22h 1074p | 829 |
| 55 | 7a5r2A2d5r2A2d5A5r2a7D5r2a7A7d3r7A7a5D | 6940 | so 2h 899p | 5 |
| 56 | 7a5r2A2d5r2A2a7D5r2a7D5r2a7A7d3r7A7a5D | 6940 | so 2h 922p | 535 |
| 57 | 7a5r2A2d5r2A2a7D5r2a7D5a3r7A7d3r7A7a5D | 6940 | so 5h 356p | 4 |
| 58 | 7a5r2A2d5r2A2a7D5r2a7D5a3r7A7a5r2D7a5D | 6940 | so 5h 379p | 834 |
| 59 | 7a5r2A2d5a3R2a7D5r2a7D5a3r7A7a5r2D7a5D | 6940 | so 9h 227p | 1065 |
| 60 | 7a5r2A2d5a3R2a7D5r2a7A7d3r7A7a5r2D7a5D | 6940 | so 14h 152p | 539 |
| 61 | 7a5r2A2d5a3R2a7D5r2a7A7d3r7A7a5r2D7a5A | 6942 | so 16h 689p | 295 |
Například rok 5777 (2016/2017 dle gregoriánského kalendáře) má molad tišri so 20h 724p. Ve výše uvedené tabulce najdeme, že jde o první rok série 04, tato série devatenácti let pak končí rokem 5795. Následující rok 5796 (2035/2036) má zase molad tišri út 13h 239p a jde tedy o první rok série 27.
Podobně jako u typů roků, lze i u sérií zhotovit tabulky, které zobrazují jaké možné série mohou předcházet a následovat danou sérii a kolikrát toto nastane v celé periodě. Vlastně se vyskytují dvě možnosti, buď je variant předchozích a následujících sérií málo - jen jednotky, nebo naopak dost - řádově stovky, výjimečně tisíce. Z tohoto důvodu chybí Sankeyovy diagramy, aby byly totiž vidět i jednotky, musel by být diagram dosti vysoký, nejméně 4000 pixel.
| předcházející možné série | série |
|---|---|
| 37:4 | 01 |
| 39:236 | 02 |
| 37:294 | |
| 38:5 | |
| 39:5 | 03 |
| 41:535 | 04 |
| 39:294 | |
| 40:4 | |
| 43:766 | 05 |
| 41:294 | |
| 42:5 | |
| 43:540 | 06 |
| 43:298 | 07 |
| 43:5 | 08 |
| 44:245 | 09 |
| 43:290 | |
| 47:299 | 10 |
| 46:534 | |
| 44:294 | |
| 48:1306 | |
| 45:5 | |
| 48:4 | 11 |
| 48:295 | 12 |
| 49:4 | |
| 49:535 | 13 |
| 51:240 | 14 |
| 49:294 | |
| 50:5 | |
| 52:1604 | 15 |
| 51:295 |
| předcházející možné série | série |
|---|---|
| 52:5 | 16 |
| 52:294 | 17 |
| 53:4 | |
| 54:535 | 18 |
| 56:241 | 19 |
| 54:294 | |
| 55:5 | |
| 58:767 | 20 |
| 56:294 | |
| 57:4 | |
| 59:766 | 21 |
| 58:67 | |
| 59:5 | 22 |
| 59:4 | 23 |
| 60:539 | 24 |
| 59:290 | |
| 61:5 | 25 |
| 02:241 | 26 |
| 61:290 | |
| 01:4 | |
| 05:771 | 27 |
| 04:833 | |
| 02:294 | |
| 03:5 | |
| 05:5 | 28 |
| 06:245 | 29 |
| 05:289 | |
| 06:295 | 30 |
| 07:4 |
| předcházející možné série | série |
|---|---|
| 09:236 | 31 |
| 07:294 | |
| 08:5 | |
| 10:1604 | 32 |
| 09:299 | |
| 10:5 | 33 |
| 10:535 | 34 |
| 13:236 | 35 |
| 12:299 | |
| 10:294 | |
| 11:4 | |
| 14:539 | 36 |
| 13:299 | |
| 15:767 | |
| 15:298 | 37 |
| 15:5 | 38 |
| 15:535 | 39 |
| 15:4 | 40 |
| 18:236 | 41 |
| 17:298 | |
| 15:290 | |
| 16:5 | |
| 18:5 | 42 |
| 18:294 | 43 |
| 20:1065 | |
| 19:540 | |
| 21:539 | 44 |
| 21:5 | 45 |
| předcházející možné série | série |
|---|---|
| 24:236 | 46 |
| 21:289 | |
| 23:4 | |
| 22:5 | |
| 24:299 | 47 |
| 27:771 | 48 |
| 26:535 | |
| 25:5 | |
| 24:294 | |
| 27:833 | 49 |
| 27:5 | 50 |
| 27:294 | 51 |
| 29:236 | |
| 28:5 | |
| 32:771 | 52 |
| 31:535 | |
| 30:299 | |
| 29:298 | |
| 32:4 | 53 |
| 32:829 | 54 |
| 32:5 | 55 |
| 34:236 | 56 |
| 33:5 | |
| 32:294 | |
| 34:4 | 57 |
| 35:539 | 58 |
| 34:295 | |
| 36:771 | 59 |
| 35:294 | |
| 36:539 | 60 |
| 36:295 | 61 |
| série | následující možné série |
|---|---|
| 01 | 26:4 |
| 02 | 27:294 |
| 26:241 | |
| 03 | 27:5 |
| 04 | 27:833 |
| 05 | 27:771 |
| 29:289 | |
| 28:5 | |
| 06 | 30:295 |
| 29:245 | |
| 07 | 31:294 |
| 30:4 | |
| 08 | 31:5 |
| 09 | 32:299 |
| 31:236 | |
| 10 | 32:1604 |
| 35:294 | |
| 34:535 | |
| 33:5 | |
| 11 | 35:4 |
| 12 | 35:299 |
| 13 | 36:299 |
| 35:236 | |
| 14 | 36:539 |
| 15 | 41:290 |
| 39:535 | |
| 37:298 | |
| 36:767 | |
| 40:4 | |
| 38:5 |
| série | následující možné série |
|---|---|
| 16 | 41:5 |
| 17 | 41:298 |
| 18 | 43:294 |
| 41:236 | |
| 42:5 | |
| 19 | 43:540 |
| 20 | 43:1065 |
| 21 | 46:289 |
| 44:539 | |
| 45:5 | |
| 22 | 46:5 |
| 23 | 46:4 |
| 24 | 47:299 |
| 46:236 | |
| 48:294 | |
| 25 | 48:5 |
| 26 | 48:535 |
| 27 | 51:294 |
| 49:833 | |
| 48:771 | |
| 50:5 | |
| 28 | 51:5 |
| 29 | 52:298 |
| 51:236 | |
| 30 | 52:299 |
| série | následující možné série |
|---|---|
| 31 | 52:535 |
| 32 | 54:829 |
| 52:771 | |
| 56:294 | |
| 55:5 | |
| 53:4 | |
| 33 | 56:5 |
| 34 | 58:295 |
| 56:236 | |
| 57:4 | |
| 35 | 59:294 |
| 58:539 | |
| 36 | 60:539 |
| 59:771 | |
| 61:295 | |
| 37 | 02:294 |
| 01:4 | |
| 38 | 02:5 |
| 39 | 04:294 |
| 02:236 | |
| 03:5 | |
| 40 | 04:4 |
| 41 | 05:294 |
| 04:535 | |
| 42 | 05:5 |
| 43 | 05:766 |
| 09:290 | |
| 07:298 | |
| 06:540 | |
| 08:5 | |
| 44 | 10:294 |
| 09:245 | |
| 45 | 10:5 |
| série | následující možné série |
|---|---|
| 46 | 10:534 |
| 47 | 10:299 |
| 48 | 12:295 |
| 10:1306 | |
| 11:4 | |
| 49 | 14:294 |
| 13:535 | |
| 12:4 | |
| 50 | 14:5 |
| 51 | 14:240 |
| 15:295 | |
| 52 | 17:294 |
| 15:1604 | |
| 16:5 | |
| 53 | 17:4 |
| 54 | 18:535 |
| 19:294 | |
| 55 | 19:5 |
| 56 | 20:294 |
| 19:241 | |
| 57 | 20:4 |
| 58 | 20:767 |
| 21:67 | |
| 59 | 24:290 |
| 21:766 | |
| 23:4 | |
| 22:5 | |
| 60 | 24:539 |
| 61 | 26:290 |
| 25:5 |
Pokud jste dočetli až sem, tak blahopřeji a vězte, že komplikovanější kalendář na tomto webu není!
Další informace:
- Lunisolární cykly
- Zlaté číslo
- Kontinuita dnů v týdnu
- Různé letopočty
- Židovský roční kalendář
- Židovský věčný kalendář
- Přesnost moladu v židovském kalendáři
- Přesnost kalendářů
- Gezerský kalendář
- Hebrejské písmo
- The Hebrew Calendar: detailní informace o židovském kalendáři (anglicky)