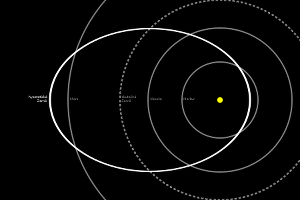
Proč jsou roční doby různě dlouhé
Jistě jste si povšimli, že přestože je rok pěkně rozdělen na čtyři roční doby, tato jednotlivá období však nejsou stejně dlouhá. Například v roce 2000 trvalo jaro 92.72 dne, léto 93.65 dne, podzim 89.88 dne a zima byla dlouhá 88.99 dne. Příčinou je eliptická dráha Země kolem Slunce. Z druhého Keplerova zákona víme, že čím je Země blíže Slunci, tím rychleji se pohybuje na své oběžné dráze kolem Slunce. Bod na této oběžné dráze, kdy je vzdálenost Země—Slunce nejmenší, se nazývá perihel. V těchto letech je Země v perihelu na začátku ledna, například v roce 2000 to bylo 3. ledna v 6:19. Je to trochu paradox, že Slunce je nám nejblíže v zimě, ale za chladné počasí v této roční době může především delší dráha slunečních paprsků v atmosféře, díky nízké poloze Slunce nad obzorem. A protože se v zimě Země pohybuje nejrychleji, je právě zima nejkratší. Naopak v létě je Země nejdále (nejvzdálenější bod na dráze se nazývá afel, v roce 2000 byla Země v afelu 4. července v 1:50), pohybuje se tedy nejpomaleji a léto trvá nejdéle. Pokud by Země obíhala kolem Slunce po kruhové dráze, všechna roční období by byla stejně dlouhá.
Navíc díky gravitačnímu působení ostatních planet dochází k pozvolnému pohybu perihelu a to ve směru oběhu Země kolem Slunce. V průběhu tisíciletí pak může někdy souhlasit poloha perihelu se začátkem roční doby, potom nastane zvláštní situace, kdy právě končící a nastávající roční doba jsou stejně dlouhé. Kolem roku -4080 Země procházela perihelem na začátku podzimu a z toho plyne, že léto (jako končící roční doba) mělo tu samou délku jako podzim. A zima pak byla stejně dlouhá jako jaro. V roce 1246 byl perihel v době zimního slunovratu a tak byl podzim zase stejně dlouhý jako zima a jaro bylo stejně dlouhé jako léto. Od tohoto roku je zima nejkratší ze všech ročních období, úplně nejkratší bude kolem roku 3500. Později, kolem roku 6433, bude Země procházet perihelem v době jarního slunovratu a pak bude zase nejkratším ročním obdobím jaro.
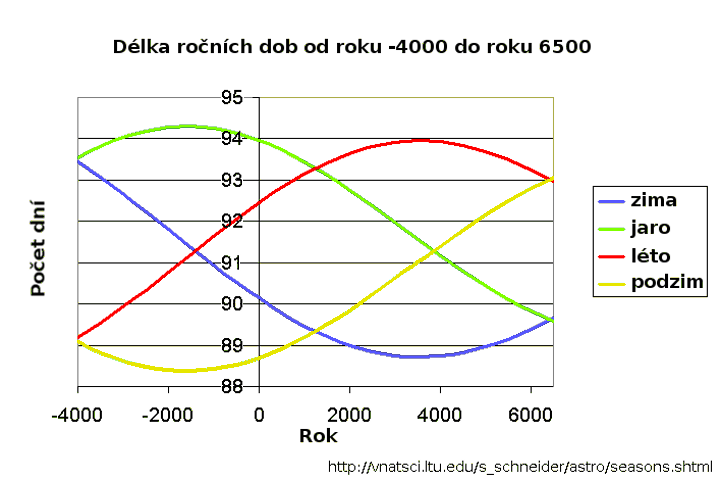
Graf různých délek ročních dob od roku -4000 do roku 6500
Pro zajímavost můžeme zkusit vypočítat, jak by se změnila délka ročních období, pokud by dráha Země kolem Slunce byla elipsa s velkou excentricitou 0.7. Ostatní elementy zemské dráhy by zůstaly stejné. Země by se pak přibližovala ke Slunci ještě více než Merkur a nejdále od Slunce by byla více jak Mars. Ovšem rok by stále trval 365¼ dne, přesně dle třetího Keplerova zákona. Definice začátku astronomických ročních dob by samozřejmě také zůstala stejná, rozhodovala by poloha Slunce na ekliptice. Například, jak by to bylo v roce 2001: Zima by v tomto případě začínala po poledni 1. ledna a trvala by pouze necelých 15 dnů. Ale vzhledem k tomu, že by Země byla Slunci dosti blízko, zima by nám určitě nebyla. Jaro by začínalo 16. ledna a trvalo něco přes 118 dnů. Léto by začínalo 14. května a trvalo by 211 dnů. Protože by Země byla naopak velmi daleko od Slunce, o nějakém teple by nešlo vůbec hovořit. Podzim by začínal 11. prosince a po 21 dnech by zase nastala zima. Za těchto podmínek, kdy jednou by byla Země rozpálená na povrchu více jak Merkur a za půl roku by zase byla chladnější než Mars, by život nebyl možný. Na tomto příkladu je však jasně patrné, že čím blíže je Země Slunci, tím je právě probíhající roční doba kratší.
Ještě větší rozdíly v délce ročních dob by nastaly, pokud by zemská dráha kolem Slunce měla excentricitu 0.967, to jest stejně jako známá Halleyova kometa. Ale jeden oběh kolem Slunce by stále trval jeden rok. Zima by pak trvala pouhých 14 hodin a léto zase plných 321 dnů!